《2025年教材完全解读八年级数学上册苏科版》

例1-1
如图3-3-2,木工师傅将一根长2.5m的梯子(AB),斜靠在与地面(OM)垂直的墙(ON)上,这时梯足B到墙底端O的距离是0.7m,当梯子的顶端A沿墙下滑0.4m到点A'时,梯足向外平移多少米？

 

答案： 解：在Rt△ABO中，AB=2.5m，BO=0.7m，
由勾股定理得：AO²=AB²-BO²=2.5²-0.7²=6.25-0.49=5.76，
∴AO=2.4m。
∵A点下移0.4m到A'，
∴A'O=AO-0.4=2.4-0.4=2m。
在Rt△A'OB'中，A'B'=2.5m，A'O=2m，
由勾股定理得：B'O²=A'B'²-A'O²=2.5²-2²=6.25-4=2.25，
∴B'O=1.5m。
∴BB'=B'O-BO=1.5-0.7=0.8m。
答：梯足向外平移0.8米。

例1-2
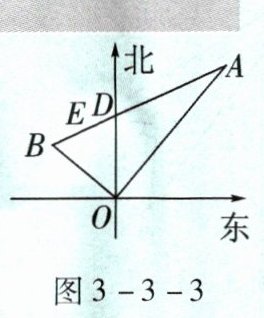
某天,暴雨突然来袭,两艘搜救艇接到消息,在海面上有遇险船只从A,B两地发出求救信号。于是,第一艘搜救艇以20n mile/h的速度离开港口O沿北偏东40°的方向向A地出发,同时,第二艘搜救艇也从港口O出发,以15n mile/h的速度向B地出发,2h后,他们同时到达各自的目标位置,如图3-3-3所示。此时,他们相距50n mile。
(1)求第二艘搜救艇的航行方向是北偏西多少度；(求∠BOD的大小)
(2)由于B地需要救援的人数较多,故需要搭载人数较少的第一艘搜救艇改道去B地支援,在从A地前往B地的过程中,与港口O最近的距离是多少？

答案：
(1)解：由题意得，OA=20×2=40(n mile)，OB=15×2=30(n mile)，AB=50(n mile)。
因为$30^{2}+40^{2}=900 + 1600=2500=50^{2}$，所以$OB^{2}+OA^{2}=AB^{2}$，则$\angle AOB=90^{\circ}$。
因为第一艘搜救艇沿北偏东$40^{\circ}$方向出发，即$\angle AOD = 40^{\circ}$，所以$\angle BOD=\angle AOB-\angle AOD=90^{\circ}-40^{\circ}=50^{\circ}$。
(2)解：过点O作$OH\perp AB$于点H，则OH的长即为所求最近距离。
由$S_{\triangle AOB}=\frac{1}{2}OA\cdot OB=\frac{1}{2}AB\cdot OH$，得$OH=\frac{OA\cdot OB}{AB}=\frac{40×30}{50}=24$ (n mile)。
答：
(1)$\angle BOD$的大小为$50^{\circ}$；
(2)最近距离是24n mile。

(1)DM=3m,BB'=10m。
(2)①求消防车在A处离楼房的距离(AD的长度)；
②求消防车两次救援移动的距离(AB的长度)。
解:
(2)①A'A=10m,A'M=9m,
所以A'D=A'M - DM=9 - 3=6(m),
在Rt△AA'D中,由勾股定理得
AD²=10² - 6²=64,所以AD=8m。
②由题意可知B'D=11 - 3=8(m),
在Rt△BB'D中,由勾股定理得
BD²=BB'² - B'D²=10² - 8²=36,
所以BD=6m,
所以AB=AD - BD=8 - 6=2(m),
所以消防车两次救援移动的距离为2m。

答案： 解:
(1)3 10
(2)①A'A=10m,A'M=9m,
所以A'D=A'M - DM=9 - 3=6(m),
在Rt△AA'D中,由勾股定理得
AD²=10² - 6²=64,所以AD=8m。
②由题意可知B'D=11 - 3=8(m),
在Rt△BB'D中,由勾股定理得
BD²=BB'² - B'D²=10² - 8²=36,
所以BD=6m,
所以AB=AD - BD=8 - 6=2(m),
所以消防车两次救援移动的距离为2m。

变式2 见答案P174
为了积极响应国家新农村建设,遂宁市某镇政府采用了移动宣讲的形式进行宣传动员。如图3-3-13,笔直公路MN的一侧,点A处有一村庄,村庄A到公路MN的距离为600m,假使宣讲车周围1000m以内能听到广播宣讲,宣讲车在公路MN上沿MN方向行驶时:
(1)请问村庄能否听到宣讲,请说明理由；
(2)如果能听到,已知宣讲车的速度是200m/min,那么村庄总共能听到多长时间的宣讲？

答 (1)由题得OA= 20×2= 40(n mile),OB= 15×2= 30(n mile)。
因为OB^2+OA^2= 30^2+40^2= 2500,AB^2= 50^2= 2500,所以OB^2+OA^2= AB^2,所以△OAB为直角三角形,所以∠AOB= 90°。
由题知∠AOD= 40°,所以∠BOD= 50°,即第二艘搜救艇的航行方向是北偏西50°。
(2)过点O作OE⊥AB,垂足为E(图略),此时OE的长度即为最近距离,由(1)知OA= 40,OB= 30,AB= 50,所以在Rt△OAB中,有S△OAB= $\frac{1}{2}$OA·OB= $\frac{1}{2}$AB·OE,即40×30= 50OE,所以OE= 24。
所以在从A地前往B地的过程中,与港口O最近的距离是24n mile。

答案：
解:
(1)村庄能听到宣讲。
理由:因为村庄A到公路MN的距离为600m＜1000m,所以村庄能听到宣讲。
(2)如图,假设当宣讲车行驶到P点开始,村庄能听到宣讲,行驶到Q点,村庄听不到宣讲。

则AP=AQ=1000m,AB=600m,
所以BP²=BQ²=1000² - 600²=800²,
所以BP=BQ=800m,
所以PQ=1600m,
1600÷200=8(min),
所以村庄总共能听到8min的宣讲。