2025年教材完全解读八年级数学上册苏科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年教材完全解读八年级数学上册苏科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第80页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
例4
如图3-1-8,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线上的点$D'$处。若AB= 3,AD= 4,求ED的长。
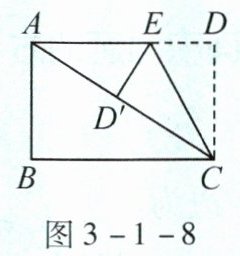
如图3-1-8,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线上的点$D'$处。若AB= 3,AD= 4,求ED的长。

答案:
【解析】:本题主要考查勾股定理的应用、折叠的性质以及一元一次方程的建立与求解。
首先,根据长方形的性质,对边相等,所以$DC = AB = 3$,$BC = AD = 4$。
接着,利用勾股定理在直角三角形$ABC$中求出对角线$AC$的长度。
根据折叠的性质,$\triangle DEC$与$\triangle D'EC$是全等的,所以$D'C = DC = 3$,$ED = ED'$。
然后,根据$AC$和$D'C$的长度求出$AD'$的长度。
设$ED = x$,则$ED' = x$,$AE = AD - ED = 4 - x$。
在直角三角形$AED'$中,利用勾股定理建立方程并求解,得出$ED$的长度。
【答案】:解:
$\because$四边形$ABCD$是长方形,
$\therefore DC = AB = 3$,$BC = AD = 4$。
在$Rt\bigtriangleup ABC$中,根据勾股定理,有
$AC^2 = AB^2 + BC^2 = 3^2 + 4^2 = 25$,
$\therefore AC = 5$。
由于折叠的性质,$\bigtriangleup DEC \cong \bigtriangleup D'EC$,
$\therefore D'C = DC = 3$,$ED = ED'$。
$\therefore AD' = AC - D'C = 5 - 3 = 2$。
设$ED = x$,则$ED' = x$,$AE = AD - ED = 4 - x$。
在$Rt\bigtriangleup AED'$中,根据勾股定理,有
$(AD')^2 + (ED')^2 = AE^2$,
即$2^2 + x^2 = (4 - x)^2$。
解这个方程,我们得到
$4 + x^2 = 16 - 8x + x^2$,
$8x = 12$,
$x = \frac{3}{2}$。
$\therefore ED$的长为$\frac{3}{2}$。
首先,根据长方形的性质,对边相等,所以$DC = AB = 3$,$BC = AD = 4$。
接着,利用勾股定理在直角三角形$ABC$中求出对角线$AC$的长度。
根据折叠的性质,$\triangle DEC$与$\triangle D'EC$是全等的,所以$D'C = DC = 3$,$ED = ED'$。
然后,根据$AC$和$D'C$的长度求出$AD'$的长度。
设$ED = x$,则$ED' = x$,$AE = AD - ED = 4 - x$。
在直角三角形$AED'$中,利用勾股定理建立方程并求解,得出$ED$的长度。
【答案】:解:
$\because$四边形$ABCD$是长方形,
$\therefore DC = AB = 3$,$BC = AD = 4$。
在$Rt\bigtriangleup ABC$中,根据勾股定理,有
$AC^2 = AB^2 + BC^2 = 3^2 + 4^2 = 25$,
$\therefore AC = 5$。
由于折叠的性质,$\bigtriangleup DEC \cong \bigtriangleup D'EC$,
$\therefore D'C = DC = 3$,$ED = ED'$。
$\therefore AD' = AC - D'C = 5 - 3 = 2$。
设$ED = x$,则$ED' = x$,$AE = AD - ED = 4 - x$。
在$Rt\bigtriangleup AED'$中,根据勾股定理,有
$(AD')^2 + (ED')^2 = AE^2$,
即$2^2 + x^2 = (4 - x)^2$。
解这个方程,我们得到
$4 + x^2 = 16 - 8x + x^2$,
$8x = 12$,
$x = \frac{3}{2}$。
$\therefore ED$的长为$\frac{3}{2}$。
变式2 见答案P172
如图3-1-13,折叠长方形纸片ABCD,使点D落在边BC上的点F处,折痕为AE。已知AB= 6 cm,BC= 10 cm,则EC的长为______cm。
如图3-1-13,折叠长方形纸片ABCD,使点D落在边BC上的点F处,折痕为AE。已知AB= 6 cm,BC= 10 cm,则EC的长为______cm。
答案:
8/3 【解析】根据长方形的性质可得 AD=BC,AB=CD,根据折叠的性质可得 AF=AD,EF=DE,利用勾股定理列式求出 BF=8 cm,再求出 FC=2 cm,然后设 DE=x cm,表示出 EC=CD - DE=(6 - x)cm,在 Rt△CEF 中,利用勾股定理列方程(6 - x)²+2²=x²,解得 x=10/3,所以 EC=CD - DE=6 - 10/3=8/3(cm)。
利用数学建模思想解题的基本步骤:(1)根据题意构造数学模型;(2)在数学模型中利用代数或几何知识求解;(3)回归实际问题作答。
例5 2024·姑苏区期末
如图3-1-9,一高层住宅发生火灾,消防车立即赶到距大厦9 m处(车尾到大厦墙面),升起云梯到火灾窗口,已知云梯长15 m,云梯底部距地面3 m,发生火灾的住户窗口距离地面有多高?
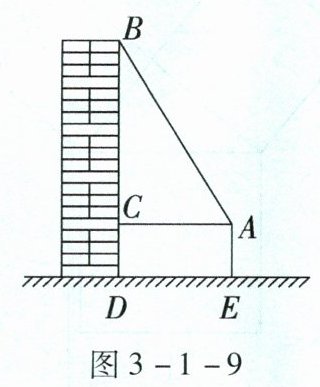
例5 2024·姑苏区期末
如图3-1-9,一高层住宅发生火灾,消防车立即赶到距大厦9 m处(车尾到大厦墙面),升起云梯到火灾窗口,已知云梯长15 m,云梯底部距地面3 m,发生火灾的住户窗口距离地面有多高?

由题意可知$AE = CD = 3m$,$AC = 9m$,$AB = 15m$;在$Rt\triangle ABC$中,根据勾股定理得$AC^{2}+BC^{2}=AB^{2}$,即$BC^{2}+9^{2}=15^{2}$,$BC^{2}=15^{2}-9^{2}=144$,所以$BC = 12m$,所以$BD = BC + CD = 12 + 3 = 15(m)$,即发生火灾的住户窗口距离地面$15m$。
答案:
【解析】:本题主要考查勾股定理的实际应用。通过构造直角三角形,利用勾股定理求出未知边长,再结合已知条件求出最终结果。
根据题意构造数学模型:
观察图形可知,$AC$、$BC$和$AB$构成一个直角三角形$ABC$,其中$AB$为云梯长度,$AC$为消防车距大厦的距离,$BC$为窗口到$C$点(云梯底部在地面的垂直投影点)的距离。
利用勾股定理求解:
在$Rt\triangle ABC$中,根据勾股定理$AC^{2}+BC^{2}=AB^{2}$。
已知$AC = 9m$,$AB = 15m$,代入可得$BC^{2}+9^{2}=15^{2}$。
即$BC^{2}=15^{2}-9^{2}=225 - 81 = 144$,
所以$BC=\sqrt{144}=12m$。
回归实际问题作答:
因为$AE = CD = 3m$(云梯底部距地面的高度),所以$BD = BC + CD = 12 + 3 = 15m$。
即发生火灾的住户窗口距离地面$15m$。
【答案】:由题意可知$AE = CD = 3m$,$AC = 9m$,$AB = 15m$;
在$Rt\triangle ABC$中,根据勾股定理得$AC^{2}+BC^{2}=AB^{2}$,
即$BC^{2}+9^{2}=15^{2}$,$BC^{2}=15^{2}-9^{2}=144$,
所以$BC = 12m$,
所以$BD = BC + CD = 12 + 3 = 15(m)$,
即发生火灾的住户窗口距离地面$15m$。
根据题意构造数学模型:
观察图形可知,$AC$、$BC$和$AB$构成一个直角三角形$ABC$,其中$AB$为云梯长度,$AC$为消防车距大厦的距离,$BC$为窗口到$C$点(云梯底部在地面的垂直投影点)的距离。
利用勾股定理求解:
在$Rt\triangle ABC$中,根据勾股定理$AC^{2}+BC^{2}=AB^{2}$。
已知$AC = 9m$,$AB = 15m$,代入可得$BC^{2}+9^{2}=15^{2}$。
即$BC^{2}=15^{2}-9^{2}=225 - 81 = 144$,
所以$BC=\sqrt{144}=12m$。
回归实际问题作答:
因为$AE = CD = 3m$(云梯底部距地面的高度),所以$BD = BC + CD = 12 + 3 = 15m$。
即发生火灾的住户窗口距离地面$15m$。
【答案】:由题意可知$AE = CD = 3m$,$AC = 9m$,$AB = 15m$;
在$Rt\triangle ABC$中,根据勾股定理得$AC^{2}+BC^{2}=AB^{2}$,
即$BC^{2}+9^{2}=15^{2}$,$BC^{2}=15^{2}-9^{2}=144$,
所以$BC = 12m$,
所以$BD = BC + CD = 12 + 3 = 15(m)$,
即发生火灾的住户窗口距离地面$15m$。
查看更多完整答案,请扫码查看


