《2025年教材完全解读八年级数学上册苏科版》

 例2-2
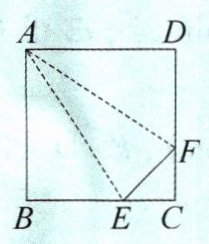
如图5-1-6,正方形ABCD的边长为4 cm,E,F分别是BC,DC边上的动点,E,F同时从点C均以1 cm/s的速度分别向点B、点D移动,当点E与点B重合时,运动停止,设运动时间为x(s),运动过程中△AEF的面积为y(cm^2)。请写出y与x之间的函数表达式,并写出自变量x的取值范围。

 

答案： 【解析】：本题考查动点问题中函数表达式的求解，关键在于根据正方形的性质和动点的运动情况，用含$x$的式子表示出相关线段的长度，进而求出$\triangle AEF$的面积$y$与运动时间$x$之间的函数关系。
已知正方形$ABCD$的边长为$4cm$，$E$，$F$分别从点$C$以$1cm/s$的速度向点$B$、点$D$移动，运动时间为$x s$。
根据路程$=$速度$×$时间，可得$CE = x cm$，$CF = x cm$。
因为$BC = 4cm$，$DC = 4cm$，所以$BE=(4 - x)cm$，$DF=(4 - x)cm$。
正方形的面积$S_{正方形ABCD}=4×4 = 16cm^2$。
$\triangle ABE$中，$AB = 4cm$，$BE=(4 - x)cm$，根据三角形面积公式$S=\frac{1}{2}×底×高$，可得$S_{\triangle ABE}=\frac{1}{2}× AB× BE=\frac{1}{2}×4×(4 - x)cm^2$。
$\triangle ADF$中，$AD = 4cm$，$DF=(4 - x)cm$，同理可得$S_{\triangle ADF}=\frac{1}{2}× AD× DF=\frac{1}{2}×4×(4 - x)cm^2$。
$\triangle ECF$中，$EC = x cm$，$FC = x cm$，所以$S_{\triangle ECF}=\frac{1}{2}× EC× FC=\frac{1}{2}x^2cm^2$。
因为$\triangle AEF$的面积$y =$正方形$ABCD$的面积$-$ $\triangle ABE$的面积$-$ $\triangle ADF$的面积$-$ $\triangle ECF$的面积，即$y = 16 - \frac{1}{2}×4×(4 - x) - \frac{1}{2}×4×(4 - x) - \frac{1}{2}x^2$，化简可得$y = -\frac{1}{2}x^2 + 4x$。
当点$E$与点$B$重合时，$CE = BC = 4cm$，因为$CE = x cm$，所以$x = 4$，又因为运动时间$x\gt0$，所以自变量$x$的取值范围是$0\lt x\leq4$。
【答案】：$y = -\frac{1}{2}x^2 + 4x(0\lt x\leq4)$

变式2 见答案P176
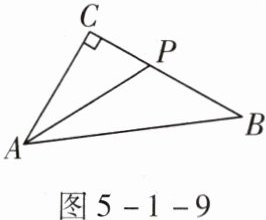
如图5-1-9,在Rt△ABC中,∠C= 90°,AC= 6,BC= 8,设P为BC上任意一点,点P不与点B,C重合,且CP= x,若$S_{\triangle APB}= y$,求：
(1)y与x之间的函数表达式；
(2)自变量x的取值范围。

答案： 2.解:
(1)因为 BC=8,CP=x,所以 BP=8-x,所以 S△ABP=1/2BP·AC=1/2×(8-x)×6=24-3x,即 y=24-3x。
(2)根据题意可得自变量 x 的取值范围为 0＜x＜8。

例3
一条公路旁依次有A,B,C三个村庄,甲、乙两人骑自行车分别从A村、B村同时出发前往C村,甲、乙之间的距离s(km)与骑行时间t(h)之间的函数关系如图5-1-7所示,下列结论中错误的是( )。

A.甲每小时比乙多骑行8 km
B.出发1.25 h后两人相遇
C.A,B两村相距10 km
D.相遇后,乙又骑了15 min或55 min时两人相距2 km
 

答案： 解：当$0\leq t\leq1.25$时，设$s=kt+b$，由图知$t=0$时$s=10$，$t=1.25$时$s=0$，代入得$\begin{cases}b=10\\1.25k + b=0\end{cases}$，解得$k=-8$，$b=10$，所以$s=-8t + 10$。
A. 由$s=-8t + 10$知甲比乙速度快$8km/h$，正确。
B. 当$t=1.25$时，$s=0$，两人相遇，正确。
C. $t=0$时$s=10$，A，B两村相距$10km$，正确。
D. 相遇后，设经过$t$小时相距$2km$，则$8t=2$，$t=0.25h=15min$；由图知乙$2.5h$到达C村，相遇时$t=1.25h$，乙剩余时间$2.5 - 1.25=1.25h$，设乙速度为$v$，相遇时乙骑行路程为$1.25v$，总路程为$1.25v + 6$（$t=2$时乙距C村$6km$），又$2v + 6=1.25v + 6 + 8×1.25$，解得$v=12km/h$，乙剩余路程$12×1.25=15km$，当乙距C村$2km$时，乙骑行$15 - 2=13km$，时间$\frac{13}{12}h\approx1.083h$，相遇后时间$\frac{13}{12}-1.25=\frac{13}{12}-\frac{3}{2}=\frac{13}{12}-\frac{18}{12}=-\frac{5}{12}h$（不合）；当乙过C村后，乙骑行$15 + 2=17km$，时间$\frac{17}{12}h\approx1.417h$，相遇后时间$\frac{17}{12}-1.25=\frac{17}{12}-\frac{15}{12}=\frac{2}{12}=\frac{1}{6}h\approx10min$，故D错误。
答：D

变式3 见答案P176
如图5-1-10①,E为长方形ABCD的边AD上一点,$BE＜BC$。点P从点B出发沿折线B-E-D运动到点D停止,点Q从点B出发沿BC运动到点C停止,它们的运动速度都是1 cm/s。现P,Q两点同时出发,设运动时间为x(s),△BPQ的面积为y(cm^2),若y与x的对应关系如图5-1-10②所示,则长方形ABCD的面积是( )。

$A.96 cm^2$
$B.84 cm^2$
$C.72 cm^2$
$D.56 cm^2$

答案：
3.C 【解析】从函数的图像和运动的过程可知,当点 P 运动到点 E 时,x=10,y=30。如图,过点 E 作 EH⊥BC,垂足为 H。
由三角形的面积公式得 y=1/2BQ×EH=1/2×10×EH=30,所以 EH=AB=6 cm,所以 AE=√(BE²-AB²)=√(10²-6²)=8(cm)。由题图②可知,当 x=14 时,点 P 与点 D 重合,所以 AD=AE+DE=8+(14 - 10)=12(cm),所以矩形的面积为 12×6=72(cm²)。

例1 2024·无锡中考
在函数$y= \sqrt{x-3}$中,自变量x的取值范围是(D)。

 

A.$x\neq3$
B.$x＞3$
C.$x＜3$
D.$x\geq3$

答案： 【解析】：
本题主要考查了函数自变量取值范围的确定，对于二次根式$\sqrt{a}$，要使其有意义，则被开方数$a\geq0$。
在函数$y = \sqrt{x - 3}$中，被开方数为$x - 3$，所以需要满足$x - 3\geq0$，解这个不等式：
$x - 3\geq0$，移项可得$x\geq3$。
【答案】：
D