第99页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
11. 计算$(\sqrt{48} - \sqrt{27}) ÷ \sqrt{3} × \sqrt{2}$的值为(
A.$\sqrt{2}$
B.$\sqrt{6}$
C.$2\sqrt{2}$
D.$\sqrt{5}$
A
)A.$\sqrt{2}$
B.$\sqrt{6}$
C.$2\sqrt{2}$
D.$\sqrt{5}$
答案:
A
12. 若$a = \sqrt{2} × (\sqrt{7} - \sqrt{2})$,则表示实数$a$的点会落在如图所示数轴的(
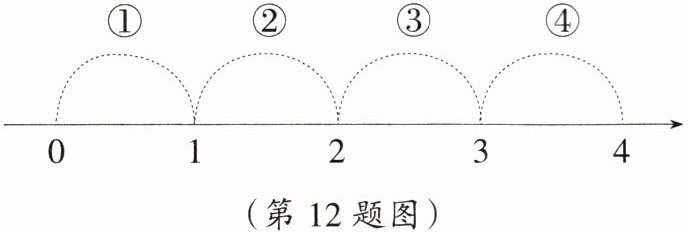
A.段①上
B.段②上
C.段③上
D.段④上
B
)
A.段①上
B.段②上
C.段③上
D.段④上
答案:
B
13. 若$x = \sqrt{2} - 1$,则代数式$x^2 + 2x + 2$的值为(
A.$3 + 2\sqrt{2}$
B.$4$
C.$3$
D.$2$
C
)A.$3 + 2\sqrt{2}$
B.$4$
C.$3$
D.$2$
答案:
C
14. 下列计算正确的是(
A.$(3 - 2\sqrt{2})(3 + 2\sqrt{2}) = 9 - 2 × 3 = 3$
B.$(2\sqrt{x} + \sqrt{y})(\sqrt{x} - \sqrt{y}) = 2x - y$
C.$(3 - \sqrt{3})^2 = 3^2 - (\sqrt{3})^2 = 6$
D.$\frac{1}{2 + \sqrt{3}} + \frac{1}{2 - \sqrt{3}} = 4$
D
)A.$(3 - 2\sqrt{2})(3 + 2\sqrt{2}) = 9 - 2 × 3 = 3$
B.$(2\sqrt{x} + \sqrt{y})(\sqrt{x} - \sqrt{y}) = 2x - y$
C.$(3 - \sqrt{3})^2 = 3^2 - (\sqrt{3})^2 = 6$
D.$\frac{1}{2 + \sqrt{3}} + \frac{1}{2 - \sqrt{3}} = 4$
答案:
D
15. 运算能力 计算:
(1) $\sqrt{3}(1 - \sqrt{3}) + \sqrt{12} + (\frac{1}{3})^{-1}$;
(2) $(\sqrt{5} - 1)(\sqrt{5} + 1) - (-\frac{1}{3})^{-2} + |1 - \sqrt{2}| - (\pi - 2)^0 + \sqrt{8}$。
(1) $\sqrt{3}(1 - \sqrt{3}) + \sqrt{12} + (\frac{1}{3})^{-1}$;
(2) $(\sqrt{5} - 1)(\sqrt{5} + 1) - (-\frac{1}{3})^{-2} + |1 - \sqrt{2}| - (\pi - 2)^0 + \sqrt{8}$。
答案:
解:
(1)原式=$\sqrt{3}-3+2\sqrt{3}+3=3\sqrt{3}$;
(2)原式=$5-1-9+\sqrt{2}-1-1+2\sqrt{2}=-7+3\sqrt{2}$.
(1)原式=$\sqrt{3}-3+2\sqrt{3}+3=3\sqrt{3}$;
(2)原式=$5-1-9+\sqrt{2}-1-1+2\sqrt{2}=-7+3\sqrt{2}$.
16. 易错题 已知$x = \sqrt{6} + 2$,$y = \sqrt{6} - 2$,求下列代数式的值。
(1) $x^2 + y^2 - xy$;
(2) $\frac{y}{x} + \frac{x}{y}$。
(1) $x^2 + y^2 - xy$;
(2) $\frac{y}{x} + \frac{x}{y}$。
答案:
解:$\because x=\sqrt{6}+2,y=\sqrt{6}-2$,
$\therefore x+y=2\sqrt{6},xy=2$.
(1)$x^{2}+y^{2}-xy=(x+y)^{2}-3xy=(2\sqrt{6})^{2}-3×2=18$;
(2)$\frac{y}{x}+\frac{x}{y}=\frac{x^{2}+y^{2}}{xy}=\frac{(x+y)^{2}-2xy}{xy}=\frac{(2\sqrt{6})^{2}-2×2}{2}=10$.
$\therefore x+y=2\sqrt{6},xy=2$.
(1)$x^{2}+y^{2}-xy=(x+y)^{2}-3xy=(2\sqrt{6})^{2}-3×2=18$;
(2)$\frac{y}{x}+\frac{x}{y}=\frac{x^{2}+y^{2}}{xy}=\frac{(x+y)^{2}-2xy}{xy}=\frac{(2\sqrt{6})^{2}-2×2}{2}=10$.
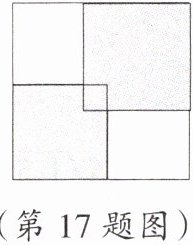
17. 数形结合思想 如图,在一个正方形的内部放置两个大小不同的正方形,其中较小的正方形的面积为$9$,重叠部分的面积为$1$,空白部分的面积为$8\sqrt{3} - 4$,求较大的正方形的面积。

答案:
解:观察可知,两个空白部分的长相等,宽也相等,易知重叠部分也为正方形,$\because$ 空白部分的面积为$8\sqrt{3}-4$,$\therefore$ 一个空白长方形面积=$4\sqrt{3}-2$,
$\because$ 较小的正方形的面积为9,重叠部分面积为1,$\therefore$ 小正方形边长=$\sqrt{9}=3$,重叠部分边长=$\sqrt{1}=1$,$\therefore$ 空白部分的宽=$3-1=2$,设空白部分长为$x$,可得$2x=4\sqrt{3}-2$,解得$x=2\sqrt{3}-1$,
$\therefore$ 较大的正方形的边长=空白部分的长+重叠部分边长=$2\sqrt{3}-1+1=2\sqrt{3}$,
$\therefore$ 较大的正方形的面积=$(2\sqrt{3})^{2}=12$.
$\because$ 较小的正方形的面积为9,重叠部分面积为1,$\therefore$ 小正方形边长=$\sqrt{9}=3$,重叠部分边长=$\sqrt{1}=1$,$\therefore$ 空白部分的宽=$3-1=2$,设空白部分长为$x$,可得$2x=4\sqrt{3}-2$,解得$x=2\sqrt{3}-1$,
$\therefore$ 较大的正方形的边长=空白部分的长+重叠部分边长=$2\sqrt{3}-1+1=2\sqrt{3}$,
$\therefore$ 较大的正方形的面积=$(2\sqrt{3})^{2}=12$.
18. 生活实践 应用意识 剪纸是一门古老的传统民间艺术,具有明显的地域特色和极高的艺术价值。为传承这一艺术,某中学举办剪纸艺术大赛,要求参赛作品的面积在$20\ dm^2$以上。如图,这是小悦同学的参赛作品(单位:$dm$)。
(1) 通过计算,判断小悦的作品是否符合参赛标准;
(2) 小涵给小悦提出建议:在参赛作品周围贴上金色彩条,这样参赛作品更漂亮,则需要彩条的长度约为多少?(彩条的宽度忽略不计,结果保留一位小数,参考数据:$\sqrt{2} \approx 1.41$)
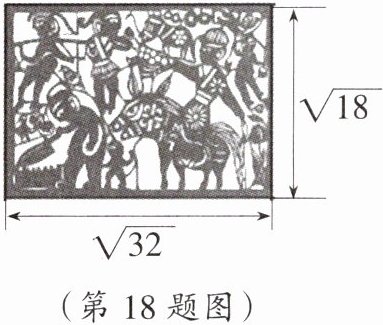
(1) 通过计算,判断小悦的作品是否符合参赛标准;
(2) 小涵给小悦提出建议:在参赛作品周围贴上金色彩条,这样参赛作品更漂亮,则需要彩条的长度约为多少?(彩条的宽度忽略不计,结果保留一位小数,参考数据:$\sqrt{2} \approx 1.41$)

答案:
解:
(1)由题意可知$\sqrt{18}×\sqrt{32}=24(dm^{2})$.$\because 24>20$,$\therefore$ 小悦的作品符合参赛标准;
(2)由题意可得$2(\sqrt{18}+\sqrt{32})=2×(3\sqrt{2}+4\sqrt{2})=14\sqrt{2}\approx19.6$ (dm),$\therefore$ 需要彩条的长度约为19.6 dm.
(1)由题意可知$\sqrt{18}×\sqrt{32}=24(dm^{2})$.$\because 24>20$,$\therefore$ 小悦的作品符合参赛标准;
(2)由题意可得$2(\sqrt{18}+\sqrt{32})=2×(3\sqrt{2}+4\sqrt{2})=14\sqrt{2}\approx19.6$ (dm),$\therefore$ 需要彩条的长度约为19.6 dm.
查看更多完整答案,请扫码查看


