《2025年全优课堂八年级数学上册冀教版》

10. 易错题 下列说法正确的是(D)
A.如果一个数的立方根是这个数本身,那么这个数一定是 0
B.一个数的立方根不是正数就是负数
C.负数没有立方根
D.一个数的立方根与这个数同号,0 的立方根是 0

答案： D

11. 若$\sqrt[3]{x}+\sqrt[3]{y}= 0$,则 x 和 y 的关系是(B)
A.$x = y = 0$
B.x 和 y 互为相反数
C.x 和 y 相等
D.不能确定

答案： B

12. 若$\sqrt[3]{a}= 2.89$,$\sqrt[3]{ab}= 28.9$,则 b 等于(B)
A.1 000 000
B.1 000
C.10
D.10 000

答案： B

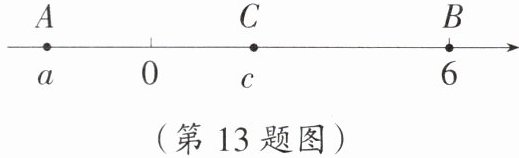
13. 数形结合思想 如图,数轴上 A,B,C 三点所表示的数分别是 a,6,c,已知$AB = 8$,$a + c = 0$,且 c 是关于 x 的一元一次方程$(m - 4)x + 16 = 0$的解的立方根,则 m 的值为(A)

A.2
B.-2
C.4
D.6

答案： A

14. 易错题 若$x - 1$是 125 的立方根,则$x - 7$的立方根是-1.

答案： -1

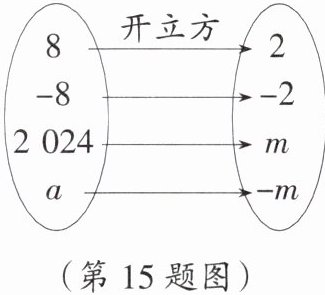
15. 根据下图中呈现的开立方运算关系,可以得出 a 的值为-2024.

答案： -2024

16. 求下各式中 x 的值.
(1)$8x^3 + 125 = 0$；
(2)$(x + 2)^3 = -27$.

答案： 解:
(1)8x³+125=0,移项得8x³=-125,系数化为1,得$x^{3}=-\frac{125}{8}$,因为$(-\frac{5}{2})^{3}=-\frac{125}{8}$,所以$x=-\frac{5}{2}$;
(2)(x+2)³=-27,因为(-3)³=-27,所以x+2=-3,所以x=-5.

17. 已知：x 的两个平方根是$a + 3与2a - 15$,且$2b - 1$的算术平方根是 3.
(1)求 a,b 的值；
(2)求$a + b - 1$的立方根.

答案： 解:
(1)
∵x的平方根是a+3与2a-15,且2b-1的算术平方根是3,
∴a+3+2a-15=0,2b-1=9.解得a=4,b=5;
(2)
∵a=4,b=5,
∴a+b-1=4+5-1=8.
∴a+b-1的立方根是2.

18. 应用意识 一个正方体的体积是$ 125 cm^3,$现将它锯成 8 块同样大小的正方体小木块.
(1)求每个小正方体的棱长；
(2)现有一张面积为$ 36 cm^2 $长方形木板,已知长方形的长是宽的 4 倍,若把以上小正方体排放在这张长方形木板上,且只排放一层,最多可以放几个小正方体？请说明理由.

答案： 解:
(1)
∵$\sqrt[3]{\frac{125}{8}}=\frac{5}{2}$,
∴每个小正方体的棱长为$\frac{5}{2}$cm;
(2)最多可放4个.理由:设长方形宽为x cm,可得4x²=36,x²=9,
∵x＞0,
∴x=3,4×3=12,12÷$\frac{5}{2}$=$\frac{24}{5}$,横排可放4个,竖排只能放1个,4×1=4(个).所以最多可放4个.

19. 类比思想 运算能力 阅读理解：我国数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题,求 59 319 的立方根.华罗庚脱口而出：39.众人惊奇,忙问计算奥妙.你知道他是怎样迅速准确地计算出结果的吗？请按照下面的分析试一试：
(1)由$10^3 = 1000$,$100^3 = 1000000$,可知$\sqrt[3]{59319}$是两位数；
(2)由 59 319 的个位数字是 9,可知$\sqrt[3]{59319}$的个位数字是 9；
(3)如果划去 59 319 后面的三位 319 得到 59,而$3^3 = 27$,$4^3 = 64$,由此确定$\sqrt[3]{59319}$的十位数字是 3.请应用以上方法计算：
$\sqrt[3]{19683}= $27；
$\sqrt[3]{175616}= $56；
$\sqrt[3]{753571}= $91.

答案： 27 56 91