第129页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
10. 如图,$P为\angle AOB$内一点,$OA= OB$,且$\triangle OPA与\triangle OPB$面积相等.求证:$\angle AOP= \angle BOP$.
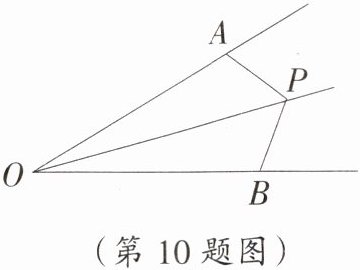

答案:
证明:如图,过点P分别作PM⊥OA交OA延长线于点M,PN⊥OB交OB延长线于点N.
∵$S_{\triangle OPA}=S_{\triangle OPB}$,
∴$\frac{1}{2}OA\cdot PM=\frac{1}{2}OB\cdot PN$,
∵OA=OB,
∴PM=PN,
∴OP为∠AOB的平分线,
∴∠AOP=∠BOP.
∵$S_{\triangle OPA}=S_{\triangle OPB}$,
∴$\frac{1}{2}OA\cdot PM=\frac{1}{2}OB\cdot PN$,
∵OA=OB,
∴PM=PN,
∴OP为∠AOB的平分线,
∴∠AOP=∠BOP.
11. 如图,在直角三角形$ABC$中,$\angle ACB= 90^{\circ}$,$AC= 6$,$BC= 8$,$AB= 10$.如果$D$,$E分别为BC$,$AB$上的动点,那么$AD+DE$的最小值是(
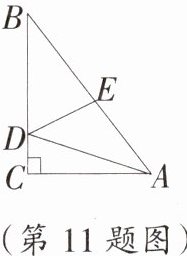
A.$8.4$
B.$9.6$
C.$10$
D.$10.8$
B
)
A.$8.4$
B.$9.6$
C.$10$
D.$10.8$
答案:
B
12. 现有如图1所示两种花纹的正方形地砖各若干块,安装在图2中两块正方形地面上,要求拼成两种不同的图案,且拼出的每种图案都满足下列条件:
①同时含有图1中的两种花纹;
②是中心对称图形.
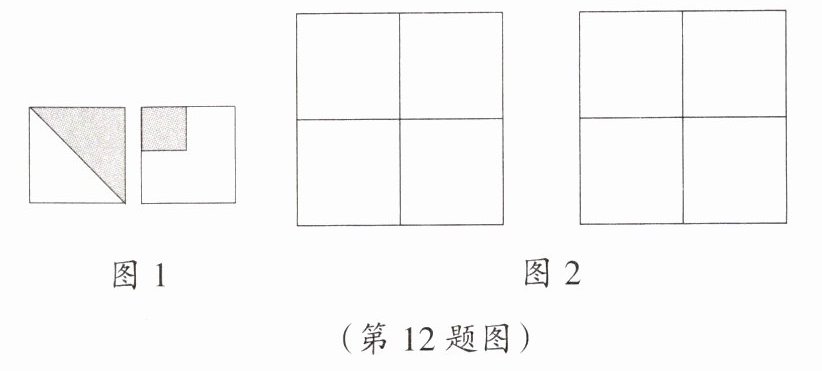
①同时含有图1中的两种花纹;
②是中心对称图形.

答案:
本题可根据中心对称图形的定义,结合题目条件进行图案设计。
中心对称图形是图形绕某一点旋转$180^{\circ}$后与原来的图形重合。
以下是两种满足条件的图案设计:
图案一:
将图$1$中第一种花纹(三角形阴影)的地砖放在左上角和右下角,第二种花纹(小正方形阴影)的地砖放在右上角和左下角。此时绕正方形地面的中心旋转$180^{\circ}$后,图形与原来的图形重合,满足中心对称图形的条件,且同时含有两种花纹。
图案二:
把图$1$中第一种花纹(三角形阴影)的地砖放在右上角和左下角,第二种花纹(小正方形阴影)的地砖放在左上角和右下角。同样,绕正方形地面的中心旋转$180^{\circ}$后,图形与原来的图形重合,也满足中心对称图形的条件,并且同时含有两种花纹。
综上,答案为(图案一):将第一种花纹地砖放左上角和右下角,第二种花纹地砖放右上角和左下角;(图案二):将第一种花纹地砖放右上角和左下角,第二种花纹地砖放左上角和右下角(答案不唯一,只要满足条件即可)。
中心对称图形是图形绕某一点旋转$180^{\circ}$后与原来的图形重合。
以下是两种满足条件的图案设计:
图案一:
将图$1$中第一种花纹(三角形阴影)的地砖放在左上角和右下角,第二种花纹(小正方形阴影)的地砖放在右上角和左下角。此时绕正方形地面的中心旋转$180^{\circ}$后,图形与原来的图形重合,满足中心对称图形的条件,且同时含有两种花纹。
图案二:
把图$1$中第一种花纹(三角形阴影)的地砖放在右上角和左下角,第二种花纹(小正方形阴影)的地砖放在左上角和右下角。同样,绕正方形地面的中心旋转$180^{\circ}$后,图形与原来的图形重合,也满足中心对称图形的条件,并且同时含有两种花纹。
综上,答案为(图案一):将第一种花纹地砖放左上角和右下角,第二种花纹地砖放右上角和左下角;(图案二):将第一种花纹地砖放右上角和左下角,第二种花纹地砖放左上角和右下角(答案不唯一,只要满足条件即可)。
13. 如图,$AB\perp BC$,$AB= BC= 2\mathrm{cm}$,曲线$OA与曲线OC关于点O$成中心对称,则$AB$,$BC$,曲线$OC$,曲线$OA$所围成图形的面积是
2
$\mathrm{cm}^{2}$.
答案:
2
14. 已知角平分线判定定理:角的内部到角两边距离相等的点在这个角的平分线上.

(1)小明认为“$PC\perp OA$,$PD\perp OB$”这两个条件可以替换为“$OC= OD$”,结论仍成立.即若$C$,$D两点分别在\angle AOB的两边OA$,$OB$上,$OC= OD$,点$P在\angle AOB$的内部,$PC= PD$,则点$P在\angle AOB$的平分线上,请你给出证明;

(2)小红认为“$PC\perp OA$,$PD\perp OB$”这两个条件可以直接去掉,结论也成立.即若点$P在\angle AOB$的内部,$PC= PD$,则点$P在\angle AOB$的平分线上.小红的想法对吗?若对请给出证明,若错请用直尺和圆规作出反例(尺规作图写出必要的文字说明或作图步骤);
(3)尺规作图:用两种方法作$\angle AOB$的平分线(写出必要的文字说明或作图步骤).
|符号语言:如图,∵$PC= PD$,$PC\perp OA$,$PD\perp OB$,∴点$P在\angle AOB$的平分线上.|$\begin{array}{l}\text { 符号语言: 如图, } \because P C= P D, \\ P C \perp O A, P D \perp O B, \\ \therefore \text { 点 } P \text { 在 } \angle A O B \text { 的 } \\ \text { 平分线上. }\end{array} $|

(1)小明认为“$PC\perp OA$,$PD\perp OB$”这两个条件可以替换为“$OC= OD$”,结论仍成立.即若$C$,$D两点分别在\angle AOB的两边OA$,$OB$上,$OC= OD$,点$P在\angle AOB$的内部,$PC= PD$,则点$P在\angle AOB$的平分线上,请你给出证明;

(2)小红认为“$PC\perp OA$,$PD\perp OB$”这两个条件可以直接去掉,结论也成立.即若点$P在\angle AOB$的内部,$PC= PD$,则点$P在\angle AOB$的平分线上.小红的想法对吗?若对请给出证明,若错请用直尺和圆规作出反例(尺规作图写出必要的文字说明或作图步骤);
(3)尺规作图:用两种方法作$\angle AOB$的平分线(写出必要的文字说明或作图步骤).
|符号语言:如图,∵$PC= PD$,$PC\perp OA$,$PD\perp OB$,∴点$P在\angle AOB$的平分线上.|$\begin{array}{l}\text { 符号语言: 如图, } \because P C= P D, \\ P C \perp O A, P D \perp O B, \\ \therefore \text { 点 } P \text { 在 } \angle A O B \text { 的 } \\ \text { 平分线上. }\end{array} $|
答案:
解:
(1)证明:如图1,
∵PO=PO,
OC=OD,PC=PD,
∴△POC≌△POD(SSS),
∴∠POA=∠POB,
∴点P在∠AOB的平分线上;
(2)小红的想法错误.如图2,OP平分∠AOB,在射线OP外取一点P',以P'为圆心,适当的长为半径作⊙P'交OA于点C,交OB于点D,满足P'C=P'D,但点P'不在∠AOB的平分线上;
(3)作图方法不唯一.如图3,在OA,OB上截取OC=OD,分别以C,D为圆心,适当的长为半径作弧两弧交于点P,作射线OP即可;如图4,分别在OA,OB上截取OC=OD,OE=OF,连接DE,CF交于点P,作射线OP即可.
(1)证明:如图1,
∵PO=PO,
OC=OD,PC=PD,
∴△POC≌△POD(SSS),
∴∠POA=∠POB,
∴点P在∠AOB的平分线上;
(2)小红的想法错误.如图2,OP平分∠AOB,在射线OP外取一点P',以P'为圆心,适当的长为半径作⊙P'交OA于点C,交OB于点D,满足P'C=P'D,但点P'不在∠AOB的平分线上;
(3)作图方法不唯一.如图3,在OA,OB上截取OC=OD,分别以C,D为圆心,适当的长为半径作弧两弧交于点P,作射线OP即可;如图4,分别在OA,OB上截取OC=OD,OE=OF,连接DE,CF交于点P,作射线OP即可.
查看更多完整答案,请扫码查看


