第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
1. 如图,若甲、乙两张卡片上分别写有一个式子,则对卡片中的式子判断正确的是(
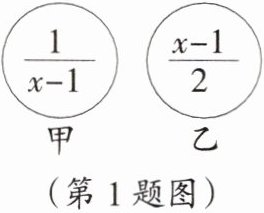
A.甲是分式,乙不是
B.乙是分式,甲不是
C.甲和乙都是分式
D.甲和乙都不是分式
A
)
A.甲是分式,乙不是
B.乙是分式,甲不是
C.甲和乙都是分式
D.甲和乙都不是分式
答案:
A
2. 下列式子一定有意义的是(
A.$\frac{2}{a}$
B.$\frac{1}{x - y}$
C.$\frac{2m}{3m + 2}$
D.$\frac{1}{a^2 + 1}$
D
)A.$\frac{2}{a}$
B.$\frac{1}{x - y}$
C.$\frac{2m}{3m + 2}$
D.$\frac{1}{a^2 + 1}$
答案:
D
3. 创新意识 如图,对于分式中的四个符号,任意改变其中的两个,分式的值不变的是(

A.①②
B.②③
C.①③
D.②④
A
)
A.①②
B.②③
C.①③
D.②④
答案:
A
4. 若分式$\frac{9x}{9 - △}$是最简分式,则$△$表示的是(
A.$3x$
B.$6$
C.$3$
D.$x$
D
)A.$3x$
B.$6$
C.$3$
D.$x$
答案:
D
5. 下列各式从左到右变形正确的是(
A.$\frac{3x^2}{6x} = \frac{x}{2}$
B.$\frac{n}{m} = \frac{n + 1}{m + 1}$
C.$\frac{n}{m} - \frac{m}{n} = \frac{n - m}{mn}$
D.$\frac{n}{m} = \frac{n^2}{m^2}$
A
)A.$\frac{3x^2}{6x} = \frac{x}{2}$
B.$\frac{n}{m} = \frac{n + 1}{m + 1}$
C.$\frac{n}{m} - \frac{m}{n} = \frac{n - m}{mn}$
D.$\frac{n}{m} = \frac{n^2}{m^2}$
答案:
A
6. 墨迹遮挡问题 如果$\frac{■}{xy + y}÷\frac{x}{2x + 2}$的运算结果为整式,则被遮挡的式子可能是(
A.$\frac{x}{3}$
B.$3xy$
C.$5y$
D.$x + y$
B
)A.$\frac{x}{3}$
B.$3xy$
C.$5y$
D.$x + y$
答案:
B
7. 易错题 关于$x的方程\frac{m}{x + 1} - \frac{2}{x + 1} = 1$的解为负数,则$m$的取值范围是(
A.$m < 2$
B.$m < 3$
C.$m < 2且3m ≠ 1$
D.$m < 3且m ≠ 2$
D
)A.$m < 2$
B.$m < 3$
C.$m < 2且3m ≠ 1$
D.$m < 3且m ≠ 2$
答案:
D
8. 下表是张亮的答卷,他的得分应是(

A.$4$分
B.$6$分
C.$8$分
D.$10$分
B
)
A.$4$分
B.$6$分
C.$8$分
D.$10$分
答案:
B
9. 如图,若$a = 6b$,$b > 0$,则$\frac{1}{a - b}·(a - \frac{2ab - b^2}{a})$的值在(

A.第①段
B.第②段
C.第③段
D.第④段
D
)
A.第①段
B.第②段
C.第③段
D.第④段
答案:
D
10. 定义新运算 对于实数$a$,$b$,定义一种新运算“☆”为:$a☆b = \frac{1}{a - b^2}$。例如:$1☆3 = \frac{1}{1 - 3^2} = - \frac{1}{8}$。则方程$x☆( - 2) = \frac{2}{x - 4} - 1$的解是(
A.$x = 7$
B.$x = 6$
C.$x = 5$
D.$x = 4$
C
)A.$x = 7$
B.$x = 6$
C.$x = 5$
D.$x = 4$
答案:
C
11. 数学文化 秦始皇统一度量衡意义重大,这一举措极大地方便了生产与生活。如图 1 和图 2,欣欣通过两把不同刻度的直尺说明了其中的原因,并进行如下探究:将两把尺子有刻度的一侧紧贴,则由两幅图可得方程(


A.$\frac{24}{32} = \frac{9}{x - 10}$
B.$\frac{24}{32} = \frac{x - 10}{9}$
C.$\frac{24}{32} = \frac{9}{x + 10}$
D.$\frac{24}{32} = \frac{x + 10}{9}$
A
)

A.$\frac{24}{32} = \frac{9}{x - 10}$
B.$\frac{24}{32} = \frac{x - 10}{9}$
C.$\frac{24}{32} = \frac{9}{x + 10}$
D.$\frac{24}{32} = \frac{x + 10}{9}$
答案:
A
查看更多完整答案,请扫码查看


