《2025年全优课堂八年级数学上册冀教版》

1. 几何直观
下列图形选自历届世博会会徽,其中是轴对称图形的是(B)

答案： B

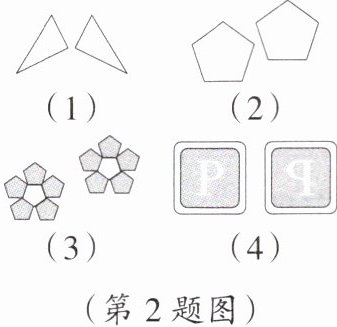
2. 分别观察图(1)~(4)中的两个图形,判断它们是否分别关于某条直线成轴对称,并说明原因.

答案： 解:图形
(1)
(4)分别关于某条直线成轴对称,因为沿某一条直线折叠,每一组的两个图形都可以完全重合;图形
(2)
(3)不成轴对称,因为找不到它们的对称轴.

3. 传统文化
围棋起源于中国,古代称之为“弈”,至今已有4000多年的历史. 以下是在棋谱中截取的四个部分,由黑白棋子摆成的图案是中心对称图形的是(C)

答案： C

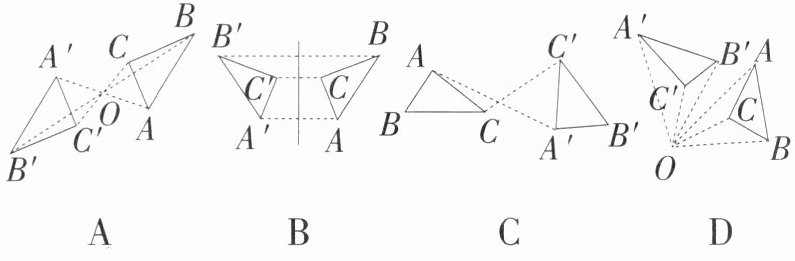
4. 下列图形中,$\triangle A^{\prime}B^{\prime}C^{\prime}与\triangle ABC$成中心对称的是(A)

答案： A

5. 如图,直角三角形$AFC和直角三角形AEB$关于虚线成轴对称,现给出下列结论：
①$\angle 1= \angle 2$；②$\triangle ANC\cong\triangle AMB$；③$CD= DN$.
其中正确的结论是①②.(填序号)

答案： ①②

6. 如图,在$\triangle ABC$中,$AC= 10$,$BC= 6$,$AB的垂直平分线交AB于点D$,交$AC于点E$,则$\triangle BCE$的周长是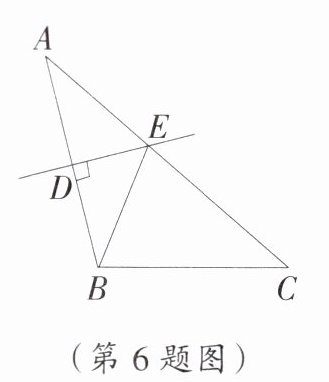16.

答案： 16

7. 如图,在$\triangle ABC$中,$DE垂直平分BC$,$BD平分\angle ABC$,$DH\perp BA$,交$BA的延长线于点H$.
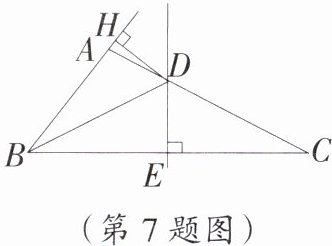
(1)若$\angle ADB= 48^{\circ}$,求$\angle BAC$的度数；
(2)若$AB= 5\mathrm{cm}$,$\triangle ABC与\triangle ABD的周长之差为8\mathrm{cm}$,且$\triangle ABD的面积为10\mathrm{cm}^{2}$,求$\triangle BDC$的面积.

答案： 解:
(1)
∵BD平分∠ABC,
∴∠ABD=∠DBC.
∵DE垂直平分BC,
∴DB=DC,
BE=CE,
∵DE=DE,
∴△DBE≌△DCE(SSS),
∴∠DBE=∠DCE,
∴∠DBC=∠C=∠ABD,
∴∠ADB=∠DBC+∠C=2∠ABD=48°,
∴∠ABD=24°,
∴∠BAC=180°-∠ABD-∠ADB=180°-24°-48°=108°;
(2)
∵DE垂直平分BC,
∴BD=DC,DE⊥BC,
∵△ABC与△ABD的周长之差为8cm,
∴(AB+BC+AD+DC)-(AB+AD+BD)=BC=8cm,
∵BD平分∠ABC,DH⊥BA,
∴DE=DH,
∵AB=5cm,△ABD的面积为10cm²,
∴$\frac{1}{2}AB\cdot DH = 10$,
∴DH=DE=$\frac{2×10}{5}$=4(cm),
∴△BDC的面积=$\frac{1}{2}BC\cdot DE=\frac{1}{2}×8×4 = 16$(cm²).

8. 易错题
下列说法中,正确的是①②④.(填序号)
①中心对称图形与成中心对称是两个不同的概念；②成中心对称与中心对称图形都只有一个对称中心；③中心对称图形是指两个图形之间的一种关系；④关于某点成中心对称的两点连线的中点刚好是对称中心.

答案： ①②④

9. 如图,$AD与BC相交于点O$,$OA= OC$,$\angle A= \angle C$,$BE= DE$.求证：$OE垂直平分BD$.

证明:在△AOB和△COD中,
$\begin{cases}∠A = ∠C,\\OA = OC,\\∠AOB = ∠COD,\end{cases}$
∴△AOB≌△COD(ASA),
∴OB=OD,
∴点O在线段BD的垂直平分线上,
∵BE=DE,
∴点E在线段BD的垂直平分线上,
∴OE垂直平分BD.

答案： 证明:在△AOB和△COD中,
$\begin{cases}∠A = ∠C,\\OA = OC,\\∠AOB = ∠COD,\end{cases}$
∴△AOB≌△COD(ASA),
∴OB=OD,
∴点O在线段BD的垂直平分线上,
∵BE=DE,
∴点E在线段BD的垂直平分线上,
∴OE垂直平分BD.