《2025年全优课堂八年级数学上册冀教版》

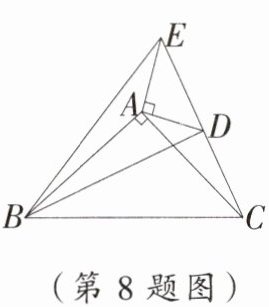
8. 如图,在△ABC,△ADE 中,∠BAC= ∠DAE= 90°,AB= AC,AD= AE,点 C,D,E 三点在同一条直线上,连接 BD,BE.以下四个结论:①BD= CE;②∠ACE+∠DBC= 45°;③BD⊥CE;④∠BAE+∠DAC= 180°.其中结论正确的个数是(D)

A.1
B.2
C.3
D.4

答案： D

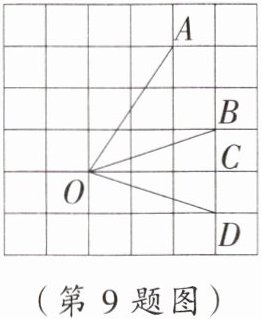
9. 如图,O,A,B,C,D 都为格点(方格纸中小正方形的顶点),∠AOC 的度数为 α,∠BOC 的度数为 β,则∠AOD 的度数可以表示为α+β.(用含 α,β 的式子表示)

答案： α+β

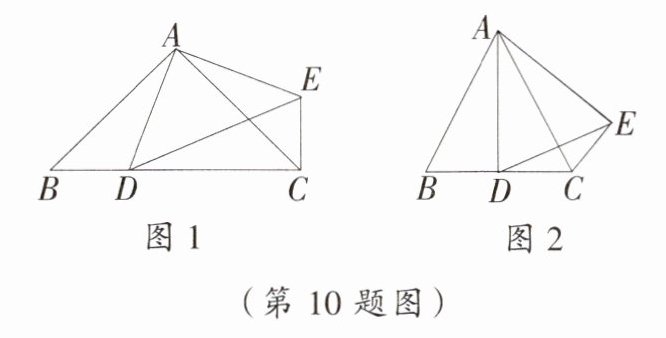
10. 推理能力 在△ABC 中,AB= AC,D 是线段 BC 上一点(不与 B,C 重合),以 AD 为一边在 AD 的右侧作△ADE,使 AD= AE,∠DAE= ∠BAC,连接 CE.
(1)如图 1,①求证:△ABD≌△ACE;
②若∠BAC= 90°,求∠BCE 的度数;
(2)如图 2,设∠BAC= α,∠BCE= β,则 α,β 之间有怎样的数量关系? 请说明理由.

答案： 解:
(1)①证明:因为∠BAC=∠DAE,
所以∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE.
在△ABD 和△ACE 中,
AB=AC,
∠BAD=∠CAE,
AD=AE,
所以△ABD≌△ACE(SAS);
②由①可得△ABD≌△ACE.
所以∠B=∠ACE.
所以∠BCE=∠ACE+∠ACB=∠B+
∠ACB=180°-∠BAC=180°-90°=90°;
(2)α+β=180°.理由:因为∠BAC=
∠DAE,所以∠BAC-∠DAC=∠DAE-
∠DAC,即∠BAD=∠CAE.
在△ABD 和△ACE 中,
AB=AC,
∠BAD=∠CAE,
AD=AE ,
所以△ABD≌△ACE(SAS),所以∠B=
∠ACE.所以∠B+∠ACB=∠ACE+
∠ACB,所以∠B+∠ACB=β.
因为α+∠B+∠ACB=180°,
所以α+β=180°.

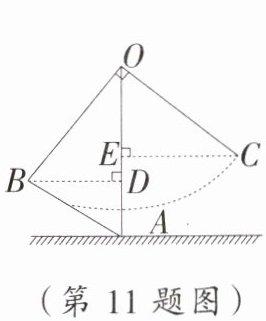
11. 抽象能力 小丽与爸妈在公园里荡秋千.如图,小丽坐在秋千的起始位置 A 处,OA 与地面垂直,两脚在地面上用力一蹬,妈妈在距地面 1 m 高的 B 处接住她后用力一推,爸爸在 C 处接住她.若妈妈与爸爸到 OA 的水平距离 BD,CE 分别为 1.4 m 和 1.8 m,∠BOC= 90°.爸爸在 C 处接住小丽时,小丽距离地面的高度是(D)

A.1 m
B.1.6 m
C.1.8 m
D.1.4 m

答案： D

12. 在一次数学活动中,为了测量一堵墙上点 A 的高度 AM,嘉淇设计了如下方案(如图):
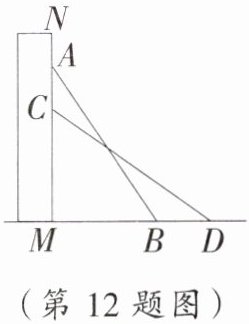
第一步:找一根长度大于 AM 的直杆,使直杆靠在墙上,且顶端与点 A 重合,测量出直杆与地面的夹角∠ABM= 50°;
第二步:使直杆顶端沿墙面竖直缓慢下滑,使得∠MDC= 40°,标记此时直杆的底端点 D;
第三步:测量地面上线段DM的长度,即为点 A 的高度.若测得 BM= 4 m,DM= 6 m,则直杆下滑的高度 AC 为2m.

答案： 40 DM 2

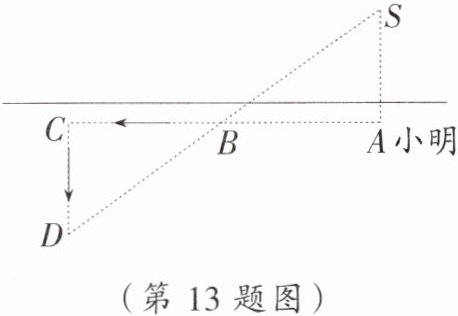
13. 应用意识 如图,小明站在堤岸的 A 点处,正对他的 S 点停有一艘游艇.他想知道这艘游艇距离他有多远,于是他沿着堤岸走到电线杆 B 旁,接着再往前走相同的距离,到达点 C.然后他向左直行,当看到电线杆与游艇在一条直线上时停下来,此时他位于点 D,量得 CD 的距离是 35 m.你知道在点 A 处小明与游艇的距离吗? 请说出他这样做的理由.

答案： 解:在 A 点处小明与游艇的距离为
35 m,理由:在△ABS 与△CBD 中,
∠A=∠C=90°,
AB=CB,
∠ABS=∠CBD,
∴△ABS≌△CBD(ASA),
∴AS=CD,
∵CD=35 m,
∴AS=CD=35 m.