《2025年全优课堂八年级数学上册冀教版》

5. 快递公司为顾客交寄的快递提供纸箱包装服务,现有三款包装纸箱,底面规格如表：

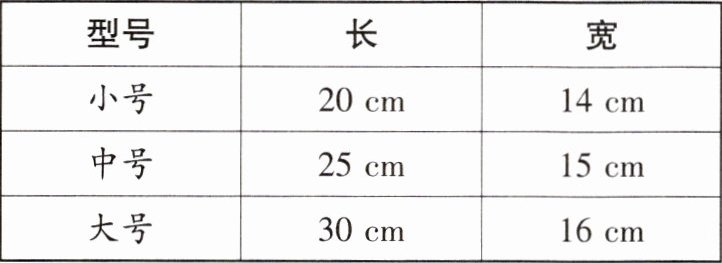
已知甲、乙两件礼品底面都是正方形,底面积分别为 90 $cm^2$,160 $cm^2$。若要将它们合在一个包装箱中寄出,底面摆放方式如图,从节约材料的角度考虑,应选择哪种底面型号的纸箱？请说明理由。

答案： 解:从节约材料的角度考虑,应选择中号底面型号的纸箱.理由如下:$\because$ 甲、乙两件礼品底面都是正方形,底面积分别为$90\ cm^2,160\ cm^2$.$\therefore$ 甲礼品的底面边长为$\sqrt{90}=3\sqrt{10}(cm)$,乙礼品的底面边长为$\sqrt{160}=4\sqrt{10}(cm)$,$\therefore3\sqrt{10}+4\sqrt{10}=7\sqrt{10}$,$\because7\sqrt{10}=\sqrt{490}$,$484＜490＜529$,$\therefore22＜7\sqrt{10}＜23$,$\because4\sqrt{10}=\sqrt{160}$,$144＜160＜169$,$\therefore12＜4\sqrt{10}＜13$,$\therefore$ 小号包装纸箱长度尺寸不够,大号包装纸箱长度尺寸偏大,中号包装纸箱长、宽尺寸适中,$\therefore$ 从节约材料的角度考虑,应选择中号底面型号的纸箱.

6. 实践操作 有一块长方形木板$ABCD$,木工甲采用如图的方式,将木板的长$AD增加2\sqrt{3}$ cm,宽$AB增加7\sqrt{3}$ cm,得到一个面积为 192 $cm^2的正方形AEFG$。
(1)求长方形木板$ABCD$的面积；
(2)木工乙想从长方形木板$ABCD$中裁出一个面积为 12 $cm^2$,宽为$\frac{\sqrt{6}}{2}$ cm 的长方形木料,求该长方形木料的长；
(3)木工丙想从长方形木板$ABCD$中截出长为 2.0 cm、宽为 1.5 cm 的长方形木条,最多能截出多少根这样的木条？

答案： 解:
(1)由添加可知:正方形$AEFG$的边长为$\sqrt{192}=8\sqrt{3}(cm)$,$\therefore AD=8\sqrt{3}-2\sqrt{3}=6\sqrt{3}(cm)$,$AB=8\sqrt{3}-7\sqrt{3}=\sqrt{3}(cm)$,$\therefore$ 长方形木板$ABCD$的面积为$6\sqrt{3}×\sqrt{3}=18(cm^2)$;
(2)该长方形木料的长为$12÷\frac{\sqrt{6}}{2}=12×\frac{2}{\sqrt{6}}=4\sqrt{6}(cm)$;
(3)$\because1.5＜\sqrt{3}＜2$,$10＜6\sqrt{3}＜11$,$\therefore$ 从长方形木板$ABCD$中截出长为$2.0\ cm$、宽为$1.5\ cm$的长方形木条,最多能截出$5$根这样的木条.