《2025年全优课堂八年级数学上册冀教版》

13. 随着人们健康意识提升,运动锻炼需求增多,越来越多的人愿意为保持健康付出更多努力.甲、乙两人相约去环形运动场进行跑步锻炼,绕环形运动场跑步一圈的里程为 400 m.
(1)甲进行变速跑训练.先以一定的速度绕运动场跑完 2 圈后立即提速 20%并以该速度跑完 2 圈后停止跑步,若提速后所用的时间比提速前少 $\frac{160}{3}$ s,求甲提速前每秒跑多少米；
(2)甲、乙同时同起点出发(甲、乙两人分别以一定的速度匀速跑步).若同向而行,640 s 后两人第一次相遇；若相向而行,$\frac{640}{9}$ s 后两人第一次相遇.已知甲比乙跑得慢,求甲、乙两人每秒各跑多少米.

答案： 解:
(1)设甲提速前每秒跑步m m,由题意,得$\frac{2×400}{m}-\frac{2×400}{(1+20\%)m}=\frac{160}{3}$.解得$m=\frac{5}{2}$.经检验,$m=\frac{5}{2}$是原方程的解,且符合题意.答:甲提速前每秒跑步$\frac{5}{2}$m;
(2)设甲、乙每秒分别跑步为x m,y m,由题意,得$\begin{cases}(x+y)×\frac{640}{9}=400,\\(y-x)×640=400,\end{cases}$解得$\begin{cases}x=\frac{5}{2},\\y=\frac{25}{8}.\end{cases}$答:甲、乙每秒分别跑步$\frac{5}{2}$m,$\frac{25}{8}$m.

14. 某校在商场购进 A,B 两种品牌的篮球,购买 A 品牌篮球花费了 2 500 元,购买 B 品牌篮球花费了 2 000 元,且购买 A 品牌篮球数量是购买 B 品牌篮球数量的 2 倍,已知购买一个 B 品牌篮球比购买一个 A 品牌篮球多花 30 元.
(1)问购买一个 A 品牌、一个 B 品牌的篮球各需多少元？
(2)该校决定再次购进 A,B 两种品牌篮球共 50 个,恰逢商场对两种品牌篮球的售价进行调整,A 品牌篮球售价比第一次购买时提高了 8%,B 品牌篮球按第一次购买时售价的九折出售,如果该校此次购买 A,B 两种品牌篮球的总费用不超过 3 060 元,那么该校此次最多可购买多少个 B 品牌篮球？

答案： 解:
(1)设购买一个A品牌的篮球需x元,则购买一个B品牌的篮球需(x+30)元,由题意,得$\frac{2500}{x}=2×\frac{2000}{x+30}$,解得x=50,经检验,x=50是原方程的解,且符合题意,则x+30=80.答:购买一个A品牌的篮球需50元,购买一个B品牌的篮球需80元;
(2)设该校此次可购买a个B品牌篮球,则购进A品牌篮球(50-a)个,由题意,得50×(1+8%)(50-a)+80×0.9a≤3060,解得a≤20,答:该校此次最多可购买20个B品牌篮球.

15. 下面是小余学习“分式方程的应用”后所作的学习笔记,请认真阅读并完成相应的任务.

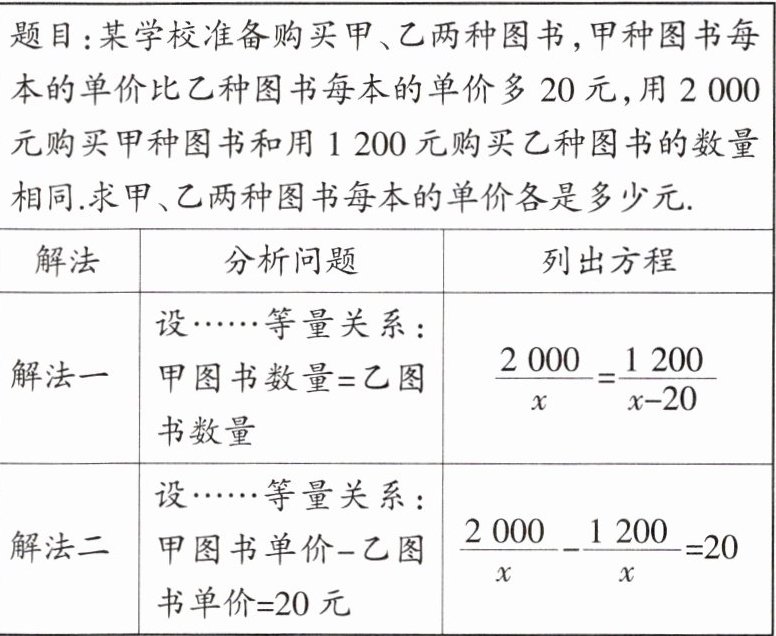
任务：
(1)解法一所列方程中的 $ x $ 表示甲种图书每本的单价,解法二所列方程中的 $ x $ 表示甲(乙)种图书购买的本数；
(2)请选择一种解法,求出甲、乙两种图书的单价.
解:选解法一:$\frac{2000}{x}=\frac{1200}{x-20}$,去分母,得2000(x-20)=1200x,整理,得5x-100=3x,解得x=50,经检验,x=50是原方程的解,且符合题意,$\therefore x-20=50-20=30$.答:甲、乙两种图书的单价分别为50元,30元.

答案： 解:
(1)甲种图书每本的单价 甲(乙)种图书购买的本数
(2)选解法一:$\frac{2000}{x}=\frac{1200}{x-20}$,去分母,得2000(x-20)=1200x,整理,得5x-100=3x,解得x=50,经检验,x=50是原方程的解,且符合题意,$\therefore x-20=50-20=30$.答:甲、乙两种图书的单价分别为50元,30元.(也可选择解法二)