《2025年全优课堂八年级数学上册冀教版》

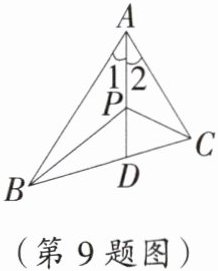
9. 如图,在△ABC 中,AB ＞ AC,∠1 = ∠2,P 为 AD 上任意一点(不与 A,D 重合),求证：AB - AC ＞ PB - PC。

答案： 证明:如图,在AB上截取AE,使AE=AC,连接PE,则BE=AB - AC.
∵AE=AC,∠1=∠2,AP=AP,
∴△AEP≌△ACP(SAS),
∴PE=PC.在△PBE中,BE＞PB - PE,即AB - AC＞PB - PC.

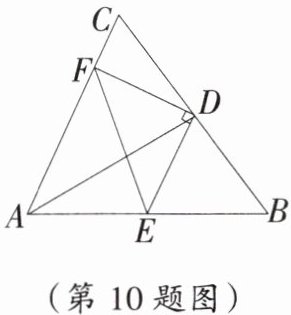
10. 如图,已知△ABC,AD 是△ABC 的中线。
(1)若 AB = 10,AC = 6,求 BC 边上的中线 AD 的取值范围；
(2)若 DE ⊥ DF 于点 D,DE 交 AB 于点 E,DF 交 AC 于点 F,连接 EF,则 EB + CF______EF。(选填“＞”“＜”或“=”)

(1)2＜AD＜8
(2)＞

答案：
(1)在题图上延长AD至M,使DM=AD,连接CM,
∴AM=2AD.
∵AD是BC边上的中线,
∴BD=CD.
∵∠CDM=∠BDA,DM=DA,
∴△CDM≌△BDA(SAS),
∴CM=AB=10.在△ACM中,由三角形的三边关系得CM - AC＜AM＜CM+AC,
∴10 - 6＜AM＜10+6,即4＜2AD＜16,
∴2＜AD＜8;
(2)＞

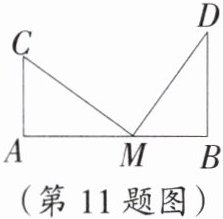
11. 应用意识 如图,两根旗杆相距 12 m,某人从点 B 沿 BA 走向点 A,一段时间后他到达点 M,此时他仰望旗杆的顶点 C 和 D,两次视线的夹角为 90°,且 CM = DM,已知旗杆 AC 的高为 3 m,该人的运动速度为 1 m/s,则这个人从点 B 到点 M 运动了3s。

答案： 3

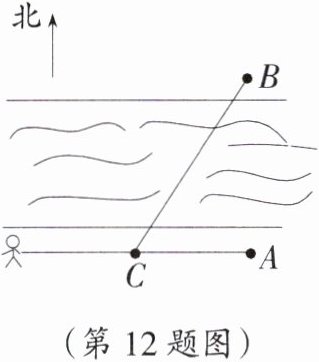
12. 如图,小刚站在河边的 A 点处,在河对岸的 B 处有一电线塔(小刚的正北方向),他想知道电线塔离他有多远,于是他向正西方向走了 20 步到达一棵树 C 处,接着再向前走了 20 步到达 D 处,然后再左转 90°直行,当小刚看到电线塔 B、树 C 与自己现处的位置 E 在一条直线时,他共走了 120 步。
(1)根据题意,画出示意图；
(2)若小刚一步约 0.5 m,请求出 A,B 两点间的距离(写出推理过程)。

答案：

(1)根据上北下南,左西右东,直角的意义,共线的条件画图如下:

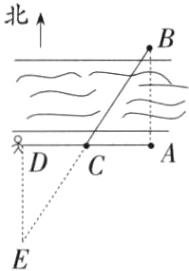
(2)在△ACB和△DCE中,∠ACB=∠DCE,AC=DC,∠BAC=∠EDC,
∴△ACB≌△DCE(ASA).
∴AB=DE=120 - 20 - 20=80(步).
∵一步约0.5m,
∴AB=80×0.5=40(m).答:A,B两点间的距离约为40m.