第14页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
1. 下列各式中是分式的是(
A.$\frac{x}{2}$
B.$x + y$
C.$\frac{5 + y}{\pi}$
D.$\frac{1}{m - 1}$
D
)A.$\frac{x}{2}$
B.$x + y$
C.$\frac{5 + y}{\pi}$
D.$\frac{1}{m - 1}$
答案:
D
2. 若分式$\frac{x^2 - y^2}{\triangle}$是最简分式,则$\triangle$表示的是(
A.$2x + 2y$
B.$(x - y)^2$
C.$x^2 + 2xy + y^2$
D.$x^2 + y^2$
D
)A.$2x + 2y$
B.$(x - y)^2$
C.$x^2 + 2xy + y^2$
D.$x^2 + y^2$
答案:
D
3. 一根蜡烛经凸透镜成一实像,物距$u$,像距$v和凸透镜的焦距f$满足关系式:$\frac{1}{u} + \frac{1}{v} = \frac{1}{f}$.已知$u和v$,则$f = $(
A.$\frac{u + v}{uv}$
B.$\frac{u - v}{uv}$
C.$\frac{uv}{u + v}$
D.$\frac{uv}{u - v}$
C
)A.$\frac{u + v}{uv}$
B.$\frac{u - v}{uv}$
C.$\frac{uv}{u + v}$
D.$\frac{uv}{u - v}$
答案:
C
4. 下列说法错误的是(
A.若式子$\frac{x - 1}{x + 1}$没有意义,则$x的取值范围是x = - 1$
B.分式$\frac{x + y}{x}中的x$,$y$都扩大为原来的2倍,那么分式的值扩大为原来的2倍
C.分式$\frac{x + 2}{|x| - 2}$的值不可能等于0
D.若$\frac{3}{x + 1}$表示一个整数,则整数$x$可取值的个数是4
B
)A.若式子$\frac{x - 1}{x + 1}$没有意义,则$x的取值范围是x = - 1$
B.分式$\frac{x + y}{x}中的x$,$y$都扩大为原来的2倍,那么分式的值扩大为原来的2倍
C.分式$\frac{x + 2}{|x| - 2}$的值不可能等于0
D.若$\frac{3}{x + 1}$表示一个整数,则整数$x$可取值的个数是4
答案:
B
5. 若$x$是非负整数,则表示$\frac{2x}{x + 2} - \frac{x^2 - 4}{(x + 2)^2}$的值的对应点落在如图所示数轴上的范围是(
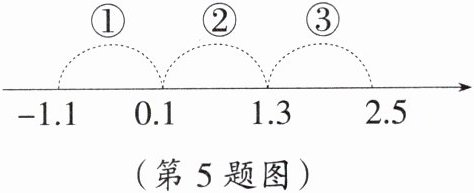
A.①
B.②
C.③
D.①或②
B
)
A.①
B.②
C.③
D.①或②
答案:
B
6. 为了练习分式的化简,张老师让同学们在分式$\frac{a^2}{a - 2}和\frac{4a - 4}{2 - a}$中间加上“+”“-”“×”“÷”四个运算符号中的任意一个后进行化简,若化简的结果为$a - 2$,则所加的运算符号为(
A.+
B.-
C.×
D.÷
A
)A.+
B.-
C.×
D.÷
答案:
A
7. 对于$M = x + 1$,$N = \frac{4x}{x + 1}$,有以下两个结论:①当$x > 0$时,$M > N$;②当$x < - 1$时,$M < N$.对于这两个结论,说法正确的是(
A.①对②不对
B.①不对②对
C.①②均对
D.①②均不对
B
)A.①对②不对
B.①不对②对
C.①②均对
D.①②均不对
答案:
B
8. 美琪在做数学作业时,不小心将式子中除号后边的代数式污染,即$\frac{4 - x^2}{3x^2 - 2xy} ÷$ 
,通过查看答案,知道答案为$\frac{x + 2}{3x - 2y}$,则被污染的代数式为(
A.$\frac{2}{x + 1}$
B.$\frac{x - 2}{x}$
C.$\frac{2 - x}{x}$
D.$\frac{x + 1}{2x - 1}$

,通过查看答案,知道答案为$\frac{x + 2}{3x - 2y}$,则被污染的代数式为(
C
)A.$\frac{2}{x + 1}$
B.$\frac{x - 2}{x}$
C.$\frac{2 - x}{x}$
D.$\frac{x + 1}{2x - 1}$
答案:
C
9. 分式$\frac{1}{2m + 2}与\frac{1}{m + 1}$的最简公分母是
2m+2
.
答案:
2m+2
10. 一个长、宽、高分别为$a$,$b$,$2r$($a$,$b为2r$的整数倍)的长方体纸盒装满了一层半径为$r$的小球,则纸盒的空间利用率(小球总体积与纸箱容积的比)为
$\frac{\pi}{6}$
. (结果保留$\pi$,球体积公式$V = \frac{4}{3}\pi r^3$).
答案:
$\frac{\pi}{6}$
11. 试卷上一个正确的式子$(\frac{1}{a + b} + \frac{1}{a - b}) ÷ \bigstar = \frac{2}{a + b}$,被小颖同学不小心滴上墨汁,被墨汁遮住部分的代数式$\bigstar$为
$\frac{a}{a-b}$
.
答案:
$\frac{a}{a-b}$
查看更多完整答案,请扫码查看


