《2025年全优课堂八年级数学上册冀教版》

7. 如图,在△AOB和△COD中,OA= OB,OC= OD,∠AOB= ∠COD,AC,BD交于点M,关于结论Ⅰ,Ⅱ,下列判断正确的是(A)
结论Ⅰ：AC= BD；
结论Ⅱ：∠CMD＞∠COD

A.Ⅰ对,Ⅱ错
B.Ⅰ错,Ⅱ对
C.Ⅰ,Ⅱ都对
D.Ⅰ,Ⅱ都错

答案： A

8. 较难题如图,在△ABC和△ABD中,BC= BD,设E是BC的中点,F是BD的中点。连接AE,AF,若∠ABC= ∠ABD,请证明△ABE≌△ABF。

答案： 证明:
∵BC=BD,E为BC的中点,F为BD的中点,
∴BE= $\frac{1}{2}$BC,BF= $\frac{1}{2}$×BD,
∴BE=BF,又
∵∠ABE=∠ABF,AB=AB,
∴△ABE≌△ABF(SAS).

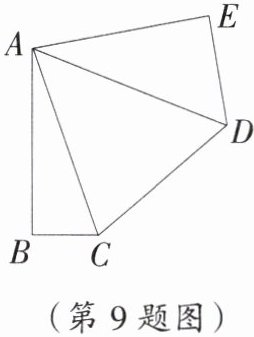
9. 截长补短法应用意识如图,某村庄有一块五边形的田地ABCDE,AB= AE= CD= 60m,∠ABC= ∠AED= 90°,连接对角线AC,AD,∠BAE= 2∠CAD。
(1)∠BAC,∠DAE与∠CAD之间的数量关系是______；
(2)为保护田内作物不被牲畜踩踏,村里决定给这块田地的五边上围一圈木栅栏,已知每米木栅栏的建造成本是50元,则建造木栅栏共需花费多少元？(提示：延长CB至点G,使BG= DE)
(3)在△ADE和△ABC区域种上小麦,已知每平方米田地的小麦播种量为11.25g,请直接写出需提前准备多少千克的小麦种。

答案：
解:
(1)∠BAC + ∠DAE=∠CAD
(2)如图，延长CB至点G,使GB=ED,连接AG.
∴BC + DE=BC + BG=GC;在△AGB与△ADE中,{AB=AE,∠ABG=∠E,GB=DE,
∴△AGB≌△ADE(SAS),
∴∠GAB=∠DAE,AG=AD.
∵∠BAC + ∠DAE=∠CAD,
∴∠BAC + ∠GAB=∠CAD,即∠GAC=∠CAD.在△AGC与△ADC中,{AC=AC,∠CAG=∠CAD,AG=AD,
∴△AGC≌△ADC(SAS),
∴GC=CD,
∴BC + ED=CD=60m.
∴五边形ABCDE的周长=3×60 + 60=240(m),
∴建造木栅栏共花费240×50=12000(元);
(3)20.25kg.

【探究与发现】(1)如图1,AD是△ABC的中线,延长AD至点E,使ED= AD,连接BE。求证：△ACD≌△EBD；
【变式与应用】(2)如图2,若EF= 10,DE= 8,试求出△DEF的中线EP的长的取值范围；
【理解与感悟】解题时,条件中若出现“中点”“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论转化到同一个三角形中；
【拓展与延伸】(3)如图3,AD是△ABC的中线,在△ABE与△ACF中,AB= AE,AC= AF,∠BAE= ∠FAC= 90°,试探究线段AD与EF的数量和位置关系,并加以证明。

答案：
解:
(1)证明:
∵AD是△ABC的中线,
∴BD=DC,在△ADC和△EDB中,{AD=ED,∠ADC=∠EDB,CD=BD,
∴△ACD≌△EBD(SAS);
(2)如图1,延长EP至点Q,使PQ=PE,连接FQ,则QE=2EP,
∵EP是△DEF的中线,
∴PD=PF,在△PDE和△PFQ中,{PD=PF,∠EPD=∠QPF,PE=PQ,
∴△PDE≌△PFQ(SAS),
∴DE=FQ=8,在△FQE中,由三角形的三边关系得EF - FQ＜QE＜EF + FQ,即10 - 8＜2EP＜10 + 8,
∴1＜EP＜9,即△DEF的中线EP的长的取值范围是1＜EP＜9;
(3)EF=2AD,AD⊥EF.证明:如图2,延长AD至点Q,使得DQ=AD,连接BQ,延长DA交EF于点P,则AQ=2AD,同
(1)得△BDQ≌△CDA(SAS),
∴∠DBQ=∠DCA,BQ=CA,
∵∠BAE=∠FAC=90°,AC=AF,AB=AE,
∴BQ=AF,
∵∠DBQ=∠DCA,
∴AC//BQ,
∴∠BAC + ∠ABQ=180°,
∵∠BAE=∠FAC=90°,
∴∠BAC + ∠EAF=180°,
∴∠ABQ=∠EAF,在△ABQ和△EAF中,{AB=EA,∠ABQ=∠EAF,BQ=AF,
∴△ABQ≌△EAF(SAS),
∴∠BAQ=∠AEF,AQ=EF,
∵AQ=2AD,
∴EF=2AD,
∵∠BAE=90°,
∴∠BAQ + ∠EAP=90°,
∴∠AEF + ∠EAP=90°,
∴∠APE=90°,
∴AD⊥EF.综上所述,EF=2AD,EF⊥AD.