《2025年全优课堂八年级数学上册冀教版》

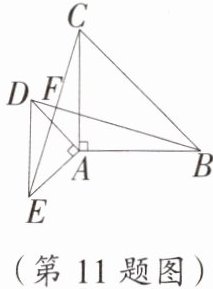
11. (12分)如图,在$\triangle ABC和\triangle ADE$中,$\angle BAC = \angle DAE = 90^{\circ}$,$AB = AC$,$AD = AE$.$BD与CE相交于点F$.
(1)求证:$\triangle BAD≌\triangle CAE$;
(2)求证:$BD\perp CE$.

答案： 证明：
(1)
∵∠BAC=∠DAE=90°，
∴∠EAC=∠DAB，
在△BAD和△CAE中，
{AD=AE，
∠DAB=∠EAC，
AB=AC，
∴△BAD≌△CAE(SAS)；
(2)设BD与AC交于点O，
∵△BAD≌△CAE，
∴∠DBA=∠ECA，
∵∠COD=∠AOB，
∴∠BFC=∠CAB=90°，
∴BD⊥CE.

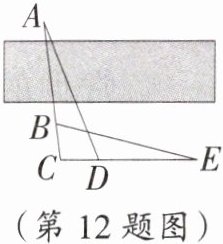
12. (16分)应用意识 如图,在河岸两侧的$A,B$两点处分别有一个电线塔,张旭想要测量这两个电线塔之间的距离,于是他在点$B所在河岸一侧的平地上取一点C$,使点$A,B,C$在一条直线上,另取一点$D$,使得$CD = BC = 5\ m$,然后测得$\angle DCB = 100^{\circ}$,$\angle ADC = 65^{\circ}$,在$CD的延长线上取一点E$,使得$\angle BEC = 15^{\circ}$.量得$CE = 32\ m$,请你帮他算一算,这两个电线塔之间的距离是多少米?

答案： 解：
∵∠DCB=100°，∠ADC=65°，
∴∠A=180°-100°-65°=15°，
∵∠BEC=15°，
∴∠BEC=∠A，
在△BCE和△DCA中，
{∠BEC=∠A，
∠BCE=∠DCA，
BC=DC，
∴△BCE≌△DCA(AAS)，
∴AC=CE，
∵BC=CD，
∴AB=AC-BC=CE-CD=32-5=27(m)，
即这两个电线塔之间的距离是27 m.

13. (18分)截长补短法 在解决线段数量关系问题时,如果条件中有角平分线,经常采用下面构造全等三角形的解题思路,如:在图1中,若$C是\angle MON的平分线OP$上一点,点$A在OM$上,此时,在$ON上截取OB = OA$,连接$BC$,根据三角形全等判定(SAS),容易构造出全等三角形$\triangle OBC和\triangle OAC$,参考上面的方法,解答下列问题:
如图2,在非等边三角形$ABC$中,$\angle B = 60^{\circ}$,$AD,CE分别是\angle BAC,\angle BCA$的平分线,且$AD,CE交于点F$,求证:$AC = AE + CD$.

答案： 证明：如图，在AC上截取AG=AE，
连接FG.
∵AD是∠BAC的平分线，
CE是∠BCA的平分线，
∴∠1=∠2，∠3=∠4.
在△AEF和△AGF中，
{AE=AG，
∠1=∠2，
AF=AF，
∴△AEF≌△AGF(SAS)，
∴∠AFE=∠AFG，
∵∠B=60°，
∴∠BAC+∠ACB=120°，
∴∠2+∠3=$\frac{1}{2}$(∠BAC+∠ACB)=60°，
∵∠AFE=∠2+∠3，
∴∠AFE=∠CFD=∠AFG=60°，
∴∠CFG=180°-∠CFD-∠AFG=60°，
∴∠CFD=∠CFG，
在△CFG和△CFD中，
{∠CFG=∠CFD，
FC=FC，
∠3=∠4，
∴△CFG≌△CFD(ASA)，
∴CG=CD，
∴AC=AG+CG=AE+CD.