《2025年初中同步练习册八年级数学上册鲁教版54制山东教育出版社》

2. 为了考察甲、乙两种农作物的长势，分别从中抽取了 10 株苗，测得苗高如下(单位：mm)：
甲：9，10，11，12，7，13，10，8，12，8；
乙：8，13，12，11，10，12，7，7，9，11.
请你经过计算后回答如下问题：
(1) 哪种农作物的 10 株苗长得比较高？
(2) 哪种农作物的 10 株苗长得比较整齐？

答案： 2.
(1)$\overline {x}_{甲}=10,\overline {x}_{乙}=10$.甲、乙的平均高度相同.
(2)$s_{甲}^{2}=3.6,s_{乙}^{2}=4.2$.甲比较整齐.

例题 为了从甲、乙两名学生中选拔一人参加今年的英语竞赛，学校每个月对他们的学习水平进行一次测验，如图所示是两人赛前 5 次测验成绩的折线统计图。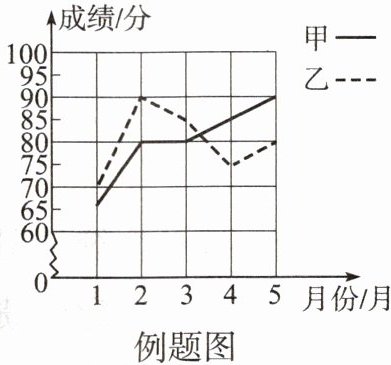
(1) 分别求出甲、乙两名学生 5 次测验成绩的平均数和方差。
(2) 如果你是他们的辅导员，应选派哪一名学生参加这次英语竞赛？请结合所学统计知识说明理由。
 

答案： 解：
(1) 由题图可知甲的 5 次成绩分别为 65，80，80，85，90；乙的 5 次成绩分别为 70，90，85，75，80。
$\overline{x}_{甲}=\frac{1}{5}×(65 + 80 + 80 + 85 + 90)=80$（分），
$\overline{x}_{乙}=\frac{1}{5}×(70 + 90 + 85 + 75 + 80)=80$（分）。
$s_{甲}^{2}=\frac{1}{5}×[(65 - 80)^{2}+(80 - 80)^{2}+(80 - 80)^{2}+(85 - 80)^{2}+(90 - 80)^{2}]=70$，
$s_{乙}^{2}=\frac{1}{5}×[(70 - 80)^{2}+(90 - 80)^{2}+(85 - 80)^{2}+(75 - 80)^{2}+(80 - 80)^{2}]=50$。
(2) 两人的平均成绩相同，虽然 $s_{甲}^{2}＞s_{乙}^{2}$，甲的波动比乙大，但由于甲呈上升趋势，特别是 后两个月甲的成绩都比乙的成绩好，因此甲比乙更有潜力，应选甲参加。