第92页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
12. (2024秋·广饶县期末)“赵爽弦图”巧妙的利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的大正方形,若图中的直角三角形的长直角边是12,大正方形的面积是169,则小正方形的面积是 (
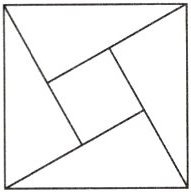
A. 25
B. 36
C. 49
D. 64
C
)
A. 25
B. 36
C. 49
D. 64
答案:
C
13. (2025春·鼓楼区期中)细心观察图形,认真分析各式,然后解答问题.
$OA_{2}^{2}=(\sqrt {1})^{2}+1=2,S_{1}=\frac {\sqrt {1}}{2}$;
$OA_{3}^{2}=1^{2}+(\sqrt {2})^{2}=3,S_{2}=\frac {\sqrt {2}}{2}$;
$OA_{4}^{2}=1^{2}+(\sqrt {3})^{2}=4,S_{3}=\frac {\sqrt {3}}{2}\cdots$
(1)请用含有n(n是正整数)的等式表示上述变规律:$OA_{n}^{2}=$
(2)求出$OA_{10}$的长.
(3)若一个三角形的面积是$\sqrt {5}$,计算说明它是第几个三角形?
(4)求出$S_{1}^{2}+S_{2}^{2}+S_{3}^{2}+\cdots +S_{10}^{2}$的值.
$OA_{2}^{2}=(\sqrt {1})^{2}+1=2,S_{1}=\frac {\sqrt {1}}{2}$;
$OA_{3}^{2}=1^{2}+(\sqrt {2})^{2}=3,S_{2}=\frac {\sqrt {2}}{2}$;
$OA_{4}^{2}=1^{2}+(\sqrt {3})^{2}=4,S_{3}=\frac {\sqrt {3}}{2}\cdots$
(1)请用含有n(n是正整数)的等式表示上述变规律:$OA_{n}^{2}=$
n
;$S_{n}=$$\frac{\sqrt{n}}{2}$
.(2)求出$OA_{10}$的长.
$\because OA_{n}^{2}=n$,$\therefore OA_{10}^{2}=10$,$\therefore OA_{10}=\sqrt{10}$(负值已舍去)
(3)若一个三角形的面积是$\sqrt {5}$,计算说明它是第几个三角形?
$\because S_{n}=\frac{\sqrt{n}}{2}=\sqrt{5}$,$\therefore \sqrt{n}=2\sqrt{5}$,$\therefore n=(2\sqrt{5})^{2}=20$,$\therefore$它是第20个三角形
(4)求出$S_{1}^{2}+S_{2}^{2}+S_{3}^{2}+\cdots +S_{10}^{2}$的值.
$S_{1}^{2}+S_{2}^{2}+S_{3}^{2}+\cdots +S_{10}^{2}=\frac{1}{4}+\frac{2}{4}+\frac{3}{4}+\frac{4}{4}+\cdots+\frac{10}{4}=\frac{1 + 2 + 3+\cdots+10}{4}=\frac{55}{4}$
答案:
(1) 由题意得: $OA_{n}^{2} = 1^{2}+(\sqrt{n - 1})^{2} = n$, $S_{n} = \frac{\sqrt{n}}{2}$, 故答案为: $n$, $\frac{\sqrt{n}}{2}$;
(2) $\because OA_{n}^{2} = n$, $\therefore OA_{10}^{2} = 10$, $\therefore OA_{10} = \sqrt{10}$ (负值已舍去);
(3) 若一个三角形的面积是 $\sqrt{5}$, $\because S_{n} = \frac{\sqrt{n}}{2} = \sqrt{5}$, $\therefore \sqrt{n} = 2\sqrt{5}$, $\therefore n = (2\sqrt{5})^{2} = 20$, $\therefore$ 它是第 20 个三角形;
(4) $S_{1}^{2}+S_{2}^{2}+S_{3}^{2}+\cdots+S_{10}^{2} = \frac{1}{4}+\frac{2}{4}+\frac{3}{4}+\frac{4}{4}+\cdots+\frac{10}{4} = \frac{1 + 2 + 3+\cdots+10}{4} = \frac{55}{4}$.
(1) 由题意得: $OA_{n}^{2} = 1^{2}+(\sqrt{n - 1})^{2} = n$, $S_{n} = \frac{\sqrt{n}}{2}$, 故答案为: $n$, $\frac{\sqrt{n}}{2}$;
(2) $\because OA_{n}^{2} = n$, $\therefore OA_{10}^{2} = 10$, $\therefore OA_{10} = \sqrt{10}$ (负值已舍去);
(3) 若一个三角形的面积是 $\sqrt{5}$, $\because S_{n} = \frac{\sqrt{n}}{2} = \sqrt{5}$, $\therefore \sqrt{n} = 2\sqrt{5}$, $\therefore n = (2\sqrt{5})^{2} = 20$, $\therefore$ 它是第 20 个三角形;
(4) $S_{1}^{2}+S_{2}^{2}+S_{3}^{2}+\cdots+S_{10}^{2} = \frac{1}{4}+\frac{2}{4}+\frac{3}{4}+\frac{4}{4}+\cdots+\frac{10}{4} = \frac{1 + 2 + 3+\cdots+10}{4} = \frac{55}{4}$.
14. (2024春·济宁期中)当直角三角形的三边长都是正整数时,我们称这三个正整数为勾股数.
(1)若a,b为一个直角三角形的两条直角边长,c为斜边长,a,b,c为勾股数,且$a=n+7,c=n+8$,n为正整数,求b的值(用含n的式子表示),并直接写出符合题意的最小的b值.
(2)当n是大于1的整数时,判断$2n,n^{2}-1,n^{2}+1$是否是勾股数,并说明理由.
(1)若a,b为一个直角三角形的两条直角边长,c为斜边长,a,b,c为勾股数,且$a=n+7,c=n+8$,n为正整数,求b的值(用含n的式子表示),并直接写出符合题意的最小的b值.
$\sqrt{2n+15}$
,5
(2)当n是大于1的整数时,判断$2n,n^{2}-1,n^{2}+1$是否是勾股数,并说明理由.
是
,理由:$\because (2n)^{2}=4n^{2}$,$(n^{2}-1)^{2}=n^{4}-2n^{2}+1$,$(n^{2}+1)^{2}=n^{4}+2n^{2}+1$,$\therefore (2n)^{2}+(n^{2}-1)^{2}=(n^{2}+1)^{2}$,$\therefore 2n$,$n^{2}-1$,$n^{2}+1$是勾股数.
答案:
(1) $a$, $b$, $c$ 为勾股数, $c$ 为斜边长, $\therefore a^{2}+b^{2} = c^{2}$. $\because a = n + 7$, $c = n + 8$, $\therefore (n + 7)^{2}+b^{2} = (n + 8)^{2}$, $\therefore b^{2} = 2n + 15$, $b = \sqrt{2n + 15}$. $\because n$, $b$ 都为正整数, $\therefore$ 当 $n = 5$ 时, $b = \sqrt{2\times5 + 15} = 5$, $\therefore$ 最小的 $b$ 值为 5;
(2) $\because (2n)^{2} = 4n^{2}$, $(n^{2}-1)^{2} = n^{4}-2n^{2}+1$, $(n^{2}+1)^{2} = n^{4}+2n^{2}+1$, $\therefore (2n)^{2}+(n^{2}-1)^{2} = (n^{2}+1)^{2}$, $\therefore 2n$, $n^{2}-1$, $n^{2}+1$ 是勾股数.
(1) $a$, $b$, $c$ 为勾股数, $c$ 为斜边长, $\therefore a^{2}+b^{2} = c^{2}$. $\because a = n + 7$, $c = n + 8$, $\therefore (n + 7)^{2}+b^{2} = (n + 8)^{2}$, $\therefore b^{2} = 2n + 15$, $b = \sqrt{2n + 15}$. $\because n$, $b$ 都为正整数, $\therefore$ 当 $n = 5$ 时, $b = \sqrt{2\times5 + 15} = 5$, $\therefore$ 最小的 $b$ 值为 5;
(2) $\because (2n)^{2} = 4n^{2}$, $(n^{2}-1)^{2} = n^{4}-2n^{2}+1$, $(n^{2}+1)^{2} = n^{4}+2n^{2}+1$, $\therefore (2n)^{2}+(n^{2}-1)^{2} = (n^{2}+1)^{2}$, $\therefore 2n$, $n^{2}-1$, $n^{2}+1$ 是勾股数.
15. (2025春·渝北区期中)著名的赵爽弦图(如图1,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为$c^{2}$,也可以表示为$4× \frac {1}{2}ab+(a-b)^{2}$,由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则$a^{2}+b^{2}=c^{2}$.
【结论探究】
(1)图2为美国第二十任总统伽菲尔德的“总统证法”,请你利用图2推导勾股定理;
【结论应用】
(2)如图3,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A,B,$AB=AC$,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A,H,B在同一条直线上),并新修一条路CH,且$CH⊥AB$.测得$CH=0.8$千米,$HB=0.6$千米,求新路CH比原路CA少多少千米?
【问题拓展】
(3)$\triangle ABC$中,$AC=10,BC=17,AB=21,CH⊥AB$,垂足为H,请直接写出CH的值.
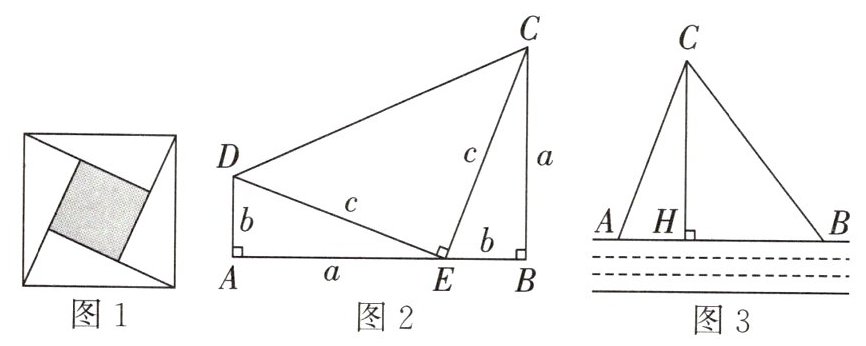
【结论探究】
(1)图2为美国第二十任总统伽菲尔德的“总统证法”,请你利用图2推导勾股定理;
【结论应用】
(2)如图3,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A,B,$AB=AC$,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A,H,B在同一条直线上),并新修一条路CH,且$CH⊥AB$.测得$CH=0.8$千米,$HB=0.6$千米,求新路CH比原路CA少多少千米?
【问题拓展】
(3)$\triangle ABC$中,$AC=10,BC=17,AB=21,CH⊥AB$,垂足为H,请直接写出CH的值.

答案:
(1) 证明: $\because$ 梯形 $ABCD$ 的面积可表示为 $\frac{1}{2}(a + b)(a + b) = \frac{1}{2}a^{2}+ab+\frac{1}{2}b^{2}$, 也可以表示为 $\frac{1}{2}ab+\frac{1}{2}ab+\frac{1}{2}c^{2}$, $\therefore \frac{1}{2}ab+\frac{1}{2}ab+\frac{1}{2}c^{2} = \frac{1}{2}a^{2}+ab+\frac{1}{2}b^{2}$, 整理, 得 $a^{2}+b^{2} = c^{2}$;
(2) 设 $AB = AC = x$ 千米, $\therefore AH = AB - BH = (x - 0.6)$ 千米, 在 $Rt\triangle ACH$ 中, 由勾股定理, 得 $CA^{2} = CH^{2}+AH^{2}$, 即 $x^{2} = 0.8^{2}+(x - 0.6)^{2}$, 解得 $x = \frac{5}{6}$, 即 $CA = \frac{5}{6}$ 千米, $\therefore CA - CH = \frac{5}{6}-0.8 = \frac{1}{30}$ (千米), 答: 新路 $CH$ 比原路 $CA$ 少 $\frac{1}{30}$ 千米;
(3) $CH = 8$. 理由: 如图, 设 $AH = y$, $\because AB = 21$, $\therefore BH = 21 - y$. $\because CH\perp AB$, 垂足为 $H$, $\therefore \triangle ACH$, $\triangle BCH$ 都是直角三角形, 在 $Rt\triangle ACH$ 中, $\because AC = 10$, $\therefore$ 由勾股定理, 得 $CH^{2} = AC^{2}-AH^{2} = 10^{2}-y^{2}$, 在 $Rt\triangle BCH$ 中, $\because BC = 17$, $\therefore$ 由勾股定理, 得 $CH^{2} = BC^{2}-BH^{2} = 17^{2}-(21 - y)^{2}$, $\therefore 10^{2}-y^{2} = 17^{2}-(21 - y)^{2}$, 解得 $y = 6$, 在 $Rt\triangle ACH$ 中, 由勾股定理, 得 $CH = \sqrt{AC^{2}-AH^{2}} = \sqrt{10^{2}-6^{2}} = 8$.
(1) 证明: $\because$ 梯形 $ABCD$ 的面积可表示为 $\frac{1}{2}(a + b)(a + b) = \frac{1}{2}a^{2}+ab+\frac{1}{2}b^{2}$, 也可以表示为 $\frac{1}{2}ab+\frac{1}{2}ab+\frac{1}{2}c^{2}$, $\therefore \frac{1}{2}ab+\frac{1}{2}ab+\frac{1}{2}c^{2} = \frac{1}{2}a^{2}+ab+\frac{1}{2}b^{2}$, 整理, 得 $a^{2}+b^{2} = c^{2}$;
(2) 设 $AB = AC = x$ 千米, $\therefore AH = AB - BH = (x - 0.6)$ 千米, 在 $Rt\triangle ACH$ 中, 由勾股定理, 得 $CA^{2} = CH^{2}+AH^{2}$, 即 $x^{2} = 0.8^{2}+(x - 0.6)^{2}$, 解得 $x = \frac{5}{6}$, 即 $CA = \frac{5}{6}$ 千米, $\therefore CA - CH = \frac{5}{6}-0.8 = \frac{1}{30}$ (千米), 答: 新路 $CH$ 比原路 $CA$ 少 $\frac{1}{30}$ 千米;
(3) $CH = 8$. 理由: 如图, 设 $AH = y$, $\because AB = 21$, $\therefore BH = 21 - y$. $\because CH\perp AB$, 垂足为 $H$, $\therefore \triangle ACH$, $\triangle BCH$ 都是直角三角形, 在 $Rt\triangle ACH$ 中, $\because AC = 10$, $\therefore$ 由勾股定理, 得 $CH^{2} = AC^{2}-AH^{2} = 10^{2}-y^{2}$, 在 $Rt\triangle BCH$ 中, $\because BC = 17$, $\therefore$ 由勾股定理, 得 $CH^{2} = BC^{2}-BH^{2} = 17^{2}-(21 - y)^{2}$, $\therefore 10^{2}-y^{2} = 17^{2}-(21 - y)^{2}$, 解得 $y = 6$, 在 $Rt\triangle ACH$ 中, 由勾股定理, 得 $CH = \sqrt{AC^{2}-AH^{2}} = \sqrt{10^{2}-6^{2}} = 8$.

查看更多完整答案,请扫码查看


