《2025年高效精练八年级数学上册苏科版》

8. (2025春·新华区期中)如图,由于大风,山坡上的树甲从点A处被拦腰折断($AB\perp$地面),其树顶端恰好落在树乙(乙$\perp$地面)的根部C处.若$AB=4$米,$BC=13$米,两棵树的水平距离为12米,则树甲折断前的高度为______19米.

答案： 如图所示：延长$AB$，过点$C$作$CD⊥AB$延长线于点$D$，由题意可得：$CD=12$米，$AB=4$米，$BC=13$米，在$Rt\triangle BCD$中，$BD=\sqrt{BC^{2}-DC^{2}}=5$米，即$AD=AB+BD=9$米，在$Rt\triangle ACD$中，$AC=\sqrt{AD^{2}+DC^{2}}=\sqrt{9^{2}+12^{2}}=15$(米)，故$AC+AB=15+4=19$(米). 答：这棵树原来的高度是19米. 故答案为：19.

9. (2024秋·宿迁期末)如图1是由四片门扇连接成的折叠门,轨道装在天花板上,图2是示意图.已知轨道$AB=110cm$,在推拉合页C或E时,滚轮D,F在轨道上移动,门完全关上时,门扇恰好贴合整条轨道.已知每小片门扇宽度均相等,则$AC=CD=DE=EF$.刚开始门扇叠合在左边,第一次向右拉开门扇,位置如图2时,$AC// DE$,$∠A=60^{\circ}$,此时门被关上部分的长AF;接着继续向右拉门扇,位置如图3时,$∠C'D'E'=90^{\circ}$,$AD':D'F'=6:8$,此时门被关上部分的长$AF'$,那么$AF'$比AF长多少厘米?

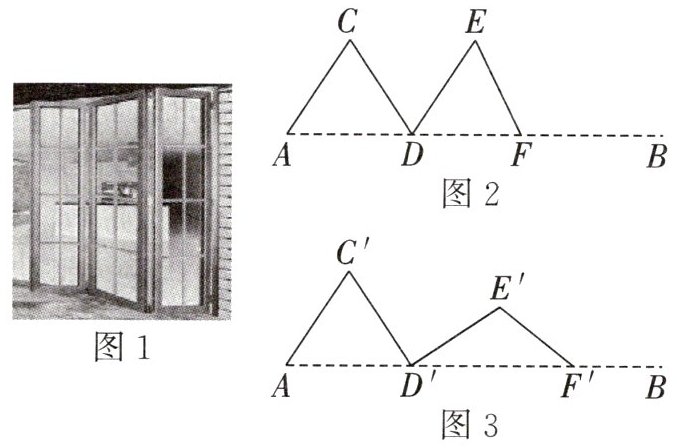
答案：
$\because$轨道$AB=110cm$，$AC=CD=DE=EF$，$\therefore AC=CD=DE=EF=\frac{1}{4}AB=\frac{55}{2}cm$，$\because ∠A=60^{\circ}$，$AC// DE$，$\therefore ∠EDF=∠A=60^{\circ}$，$\therefore \triangle ACD$和$\triangle DEF$是等边三角形，$\therefore AD=DF=\frac{55}{2}cm$，$\therefore AF=55cm$. 作$C'M⊥AB$于点$M$，$E'N⊥AB$于点$N$，$\therefore ∠C'MD'=∠E'ND'=90^{\circ}$，$MD'=\frac{1}{2}AD'$，$ND'=\frac{1}{2}D'F'$，$\therefore ∠MC'D'+∠MD'C'=90^{\circ}$，$\because ∠C'D'E'=90^{\circ}$，$\therefore ∠MD'C'+∠ND'E'=90^{\circ}$，$\therefore ∠MC'D'=∠ND'E'$，又$\because C'D'=D'E'$，$\therefore \triangle C'MD'\cong \triangle D'NE'(AAS)$，$\therefore C'M=D'N$，$\because AD':D'F'=6:8$，$\therefore MD':ND'=6:8$，$\therefore MD':C'M=6:8$，设$MD'$为$6xcm$，则$C'M$为$8xcm$，在$Rt\triangle C'D'M$中，$C'M^{2}+MD'^{2}=C'D'^{2}$，$\therefore C'M=22cm$，$D'M=\frac{33}{2}cm$，$\therefore D'N=22cm$，$\therefore AD'=33cm$，$D'F'=44cm$，$\therefore AF'$比$AF$长$33+44-55=22(cm)$.

10. (2025春·思明区期中)图1是某品牌婴儿车,图2为其简化结构示意图.根据安全标准需满足$AB\perp BD$,现测得$AB=CD=6dm$,$BC=3dm$,$AD=9dm$,其中BC与CD之间由一个固定为$90^{\circ}$的零件连接(即$∠BCD=90^{\circ}$),通过计算说明该车是否符合安全标准.

该车符合安全标准，理由：在$Rt\triangle ABD$中，由勾股定理得：$BD^{2}=AD^{2}-AB^{2}=9^{2}-6^{2}=45$，$\because BC=3dm$，$CD=6dm$，$\therefore BC^{2}+CD^{2}=3^{2}+6^{2}=45$，$\therefore BC^{2}+CD^{2}=BD^{2}$，$\therefore \triangle BCD$是直角三角形，且$∠BCD=90^{\circ}$，$\therefore BC⊥CD$，$\therefore$该车符合安全标准.

答案： 该车符合安全标准，理由：在$Rt\triangle ABD$中，由勾股定理得：$BD^{2}=AD^{2}-AB^{2}=9^{2}-6^{2}=45$，$\because BC=3dm$，$CD=6dm$，$\therefore BC^{2}+CD^{2}=3^{2}+6^{2}=45$，$\therefore BC^{2}+CD^{2}=BD^{2}$，$\therefore \triangle BCD$是直角三角形，且$∠BCD=90^{\circ}$，$\therefore BC⊥CD$，$\therefore$该车符合安全标准.

11. (2024秋·镇江期中)小明在探究勾股数的规律时关注到这样一组勾股数:3,4,5;5,12,13;7,24,25…,他发现这些勾股数都是由一个大于1的奇数和两个连续的正整数组成.
(1)小明根据他的发现写出了这样一组数:9,40,41,这是一组勾股数吗,请给出证明.
(2)为了进一步探究这组勾股数的构成规律,小明设这样的勾股数为m,n,$n+1$(m为大于1的奇数,且$m\lt n$),他猜想是否可以用m表示出n.若可以,请帮小明完成他的猜想,若不可以,请说明理由.
(3)当奇数$m=17$时,请直接写出这组勾股数.

答案：
(1)9，40，41是一组勾股数，理由如下：$\because 9^{2}+40^{2}=81+1600=1681$，$41^{2}=1681$，$\therefore 9^{2}+40^{2}=41^{2}$，$\therefore$9，40，41是一组勾股数；
(2)可以用$m$表示出$n$，理由如下：$\because m^{2}+n^{2}=(n+1)^{2}$，$\therefore m^{2}=(n+1)^{2}-n^{2}=2n+1$，$\therefore n=\frac{m^{2}-1}{2}$；
(3)当奇数$m=17$时，$n=\frac{m^{2}-1}{2}=\frac{17^{2}-1}{2}=144$，$\therefore$这组勾股数是17，144，145.