《2025年高效精练八年级数学上册苏科版》

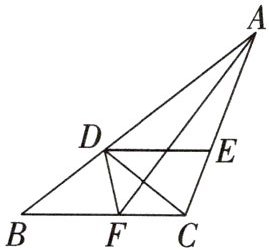
15. (2025春·雁塔区阶段考)如图所示,在 $ \triangle ABC $ 中,$ D $ 是 $ AB $ 上的一点,且 $ AD = AC $,$ DE // BC $,$ CD $ 平分 $ \angle EDF $,求证:$ AF $ 垂直平分 $ CD $.

答案： 证明:
∵ DE//BC,
∴ ∠CDE = ∠DCF.
∵ CD 平分 ∠EDF,
∴ ∠CDF = ∠CDE,
∴ ∠CDF = ∠DCF,
∴ DF = CF,
∴ 点 F 在线段 CD 的垂直平分线上.
∵ AD = AC,
∴ 点 A 在线段 CD 的垂直平分线上,
∴ AF 垂直平分 CD.

16. (2024春·秦都区期中)如图,在 $ \triangle ABC $ 中,$ AC \perp BC $,$ AD $ 平分 $ \angle BAC $,$ DE \perp AB $ 于点 $ E $,求证:直线 $ AD $ 是 $ CE $ 的垂直平分线.

证明: ∵ DE⊥AB, AC⊥BC, ∴ ∠AED = ∠ACB = 90°. 又 ∵ AD 平分 ∠BAC, ∴ ∠DAE = ∠DAC. ∵ AD = AD, 在 △AED 和 △ACD 中, $\begin{cases} ∠AED = ∠ACD, \\ ∠DAE = ∠DAC, \\ AD = AD, \end{cases}$ ∴ △AED ≌ △ACD (AAS), ∴ AE = AC, DE = DC, ∴ AD 平分线段 EC, 即直线 AD 是线段 CE 的垂直平分线.

答案： 证明:
∵ DE⊥AB, AC⊥BC,
∴ ∠AED = ∠ACB = 90°. 又
∵ AD 平分 ∠BAC,
∴ ∠DAE = ∠DAC.
∵ AD = AD, 在 △AED 和 △ACD 中, $\begin{cases} ∠AED = ∠ACD, \\ ∠DAE = ∠DAC, \\ AD = AD, \end{cases}$
∴ △AED ≌ △ACD (AAS),
∴ AE = AC, DE = DC,
∴ AD 平分线段 EC, 即直线 AD 是线段 CE 的垂直平分线.

17. (2024秋·防城区期中)【教材呈现】以下是苏科版八年级上册数学教材第 35 页的部分内容.
如图 1,在四边形 $ ABCD $ 中,$ AD = CD $,$ AB = CB $. 我们把两组邻边分别相等的四边形叫作“筝形”.
【性质探究】
(1) 如图 1,连接筝形 $ ABCD $ 的对角线 $ AC $,$ BD $ 交于点 $ O $,试探究筝形 $ ABCD $ 的性质,并填空:对角线 $ AC $,$ BD $ 的位置关系是:AC⊥BD;$ AO $ 与 $ CO $ 的数量关系是:AO = CO.
【知识应用】
秀秀想要做一个“筝形”风筝,她先固定中间的“十字架”,再确定四周.
(2) ①从数学的角度看,秀秀确定“十字架”对角线 $ EG $ 和 $ HF $ 时应满足的条件是EG 垂直平分 HF;
②借助图 2 以及①中所写条件,说明四边形 $ EHGF $ 是“筝形”.
【应用拓展】
(3) 在“筝形”风筝 $ EHGF $ 中,已知 $ EG = 60 \text{ cm} $,$ HF = 40 \text{ cm} $,求“筝形”风筝 $ EHGF $ 的面积.∵ 四边形 EHGF 是筝形, ∴ EG⊥HF, ∴ “筝形”风筝 EHGF 的面积 = △EHF 的面积 + △HGF 的面积 = $\frac{1}{2}$HF·EI + $\frac{1}{2}$HF·IG = $\frac{1}{2}$HF·(EI + IG) = $\frac{1}{2}$HF·EG = $\frac{1}{2}$×40×60 = 1200(cm²)

答案：
(1) AC⊥BD, AO = CO
(2) ① EG 垂直平分 HF; ② 证明:
∵ EG 垂直平分 HF,
∴ EH = EF, GH = GF,
∴ 四边形 EHGF 是个“筝形”;
(3)
∵ 四边形 EHGF 是筝形,
∴ EG⊥HF,
∴ “筝形”风筝 EHGF 的面积 = △EHF 的面积 + △HGF 的面积 = $\frac{1}{2}$HF·EI + $\frac{1}{2}$HF·IG = $\frac{1}{2}$HF·(EI + IG) = $\frac{1}{2}$HF·EG = $\frac{1}{2}$×40×60 = 1200(cm²).