第64页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
11. 有一个数值转换器,原理如图所示,当输入的数$x$为$-512$时,输出的数$y$的值是 (
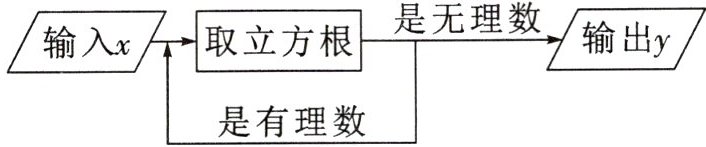
A. $-\sqrt[3]{2}$
B. $\sqrt[3]{2}$
C. $-2$
D. $2$
A
)
A. $-\sqrt[3]{2}$
B. $\sqrt[3]{2}$
C. $-2$
D. $2$
答案:
A
12. (2024秋·邓州市期末)请你写出一个无理数$a$,使得$1<a<3$,则$a$为______
$\sqrt{2}$(答案不唯一)
.
答案:
$\sqrt{2}$(答案不唯一).
13. (2024秋·邵东市期末)在实数$0.23,\pi,-\sqrt{2},\frac{22}{7},0.30030003,\sqrt{3}$中,无理数的个数是______
3
个.
答案:
3
14. (2024·赤峰)写出一个比$\sqrt{5}$小的整数
2(答案不唯一)
.
答案:
2(答案不唯一).
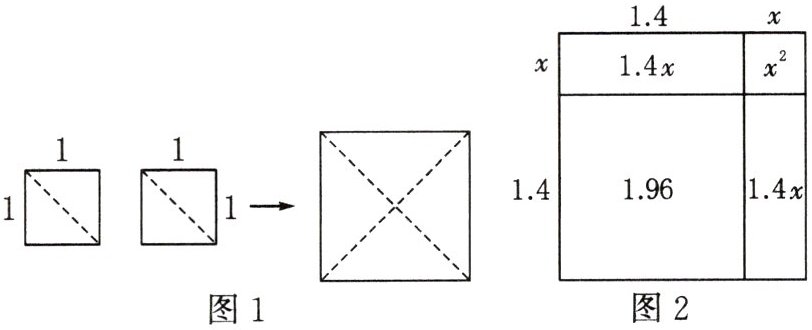
15. (2025春·厦门阶段考)问题情境:$\sqrt{2}$有多大? 如图1,教材中用两个面积为1的小正方形分别沿对角线剪开,拼成一个面积是2的大正方形,则大正方形的边长为$\sqrt{2}$.
(1)探究过程:因为$1.4^{2}=1.96,1.5^{2}=2.25$,所以$1.4<\sqrt{2}<1.5$.设$\sqrt{2}=1.4+x$,将边长为$\sqrt{2}$的正方形分成如图2所示的四部分.由面积公式,可得$x^{2}+2.8x+1.96=2$,因为$x$值很小,所以$x^{2}$更小,略去$x^{2}$,解得$x\approx0.014$(保留到0.001),即$\sqrt{2}\approx$______.
(2)理解应用:现在仿照上面的探究“$\sqrt{2}$有多大?”的过程,请你写出探究“$\sqrt{7}$有多大?”的过程.(结果均保留到0.001)
(1)探究过程:因为$1.4^{2}=1.96,1.5^{2}=2.25$,所以$1.4<\sqrt{2}<1.5$.设$\sqrt{2}=1.4+x$,将边长为$\sqrt{2}$的正方形分成如图2所示的四部分.由面积公式,可得$x^{2}+2.8x+1.96=2$,因为$x$值很小,所以$x^{2}$更小,略去$x^{2}$,解得$x\approx0.014$(保留到0.001),即$\sqrt{2}\approx$______.
(2)理解应用:现在仿照上面的探究“$\sqrt{2}$有多大?”的过程,请你写出探究“$\sqrt{7}$有多大?”的过程.(结果均保留到0.001)

答案:
(1) 1.414
(2) $\because 2.6^{2}=6.76$,$2.7^{2}=7.29$,$\therefore 2.6<\sqrt{7}<2.7$,设$\sqrt{7}=2.6+x$,画出示意图,由面积公式,可得$x^{2}+5.2x+6.76=7$.$\because x$值很小,$\therefore x^{2}$更小,解得$x\approx 0.046$(保留到 0.001),即$\sqrt{7}\approx 2.646$;

(1) 1.414
(2) $\because 2.6^{2}=6.76$,$2.7^{2}=7.29$,$\therefore 2.6<\sqrt{7}<2.7$,设$\sqrt{7}=2.6+x$,画出示意图,由面积公式,可得$x^{2}+5.2x+6.76=7$.$\because x$值很小,$\therefore x^{2}$更小,解得$x\approx 0.046$(保留到 0.001),即$\sqrt{7}\approx 2.646$;

16. (2024秋·城关区期末)新定义:若无理数$\sqrt{T}$的被开方数($T$为正整数)满足$n^{2}<T<(n+1)^{2}$(其中$n$为正整数),则称无理数$\sqrt{T}$的“青一区间”为$(n,n+1)$;同理规定无理数$-\sqrt{T}$的“青一区间”为$(-n-1,-n)$,例如:因为$1^{2}<2<2^{2}$,所以$\sqrt{2}$的“青一区间”为$(1,2)$,$-\sqrt{2}$的“青一区间”为$(-2,-1)$,请回答下列问题:
(1)$\sqrt{17}$的“青一区间”为
(2)实数$x,y$,满足关系式:$\sqrt{x-3}+|2025+(y-4)^{2}|=2025$,求$\sqrt{xy}$的“青一区间”.
(1)$\sqrt{17}$的“青一区间”为
$(4,5)$
;$-\sqrt{23}$的“青一区间”为$(-5,-4)$
;(2)实数$x,y$,满足关系式:$\sqrt{x-3}+|2025+(y-4)^{2}|=2025$,求$\sqrt{xy}$的“青一区间”.
$(3,4)$
答案:
(1) $(4,5)$ $(-5,-4)$
(2) $\because \sqrt{x-3}+|2025+(y-4)^{2}|=2025$,$\therefore \sqrt{x-3}+2025+(y-4)^{2}=2025$,即$\sqrt{x-3}+(y-4)^{2}=0$,$\therefore x=3$,$y=4$,$\therefore \sqrt{xy}=\sqrt{12}$.$\because 3^{2}<12<4^{2}$,$\therefore \sqrt{xy}$的“青一区间”为$(3,4)$.
(1) $(4,5)$ $(-5,-4)$
(2) $\because \sqrt{x-3}+|2025+(y-4)^{2}|=2025$,$\therefore \sqrt{x-3}+2025+(y-4)^{2}=2025$,即$\sqrt{x-3}+(y-4)^{2}=0$,$\therefore x=3$,$y=4$,$\therefore \sqrt{xy}=\sqrt{12}$.$\because 3^{2}<12<4^{2}$,$\therefore \sqrt{xy}$的“青一区间”为$(3,4)$.
查看更多完整答案,请扫码查看


