《2025年高效精练八年级数学上册苏科版》

12. (1)小明家新房入户门门框的尺寸如图1所示,一块长3m,宽2.2m的装修木板能否从门框内通过? 请通过计算进行说明.(参考数据:$\sqrt{5}\approx 2.236$)
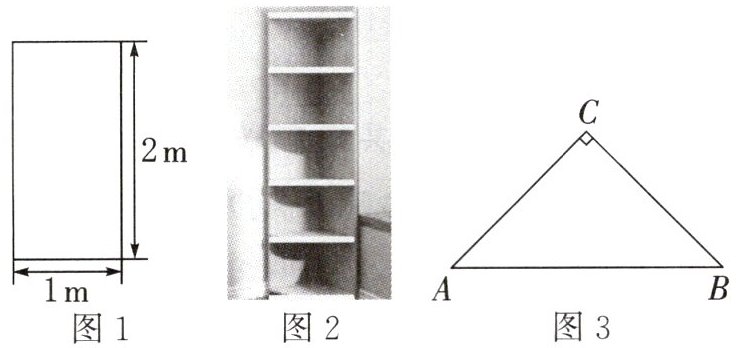
能，理由是：如图，连接 $AC$，则 $AC$ 与 $AB$，$BC$ 构成直角三角形，根据勾股定理得，则 $AC = \sqrt{AB^{2}+BC^{2}} = \sqrt{1^{2}+2^{2}} = \sqrt{5} \approx 2.236$，$\because 2.2$ m $＜ 2.236$ m，$\therefore$ 该长方形能从内框内通过（将该长方形的宽沿着 $AC$ 斜着进去）
(2)新房装修完后,要在卧室墙角放一个横截面是一个等腰直角三角形(图2)的立柜,截面如图3,腰长为$\sqrt{2}$m,小明家通往卧室的过道宽为1.05m,这个立柜能通过吗? 请通过计算进行说明.
能，理由是：过点 $C$ 作 $CD \perp AB$，则 $\triangle ACD$ 是等腰直角三角形，即 $AD = CD$，$\because AC = \sqrt{2}$，$\therefore CD^{2}+AD^{2}=AC^{2}$，$2CD^{2}=(\sqrt{2})^{2}$，$\because CD^{2}=1$，$CD = 1 ＜ 1.05$，这个立柜能通过过道.

答案：
(1) 能，理由是：如图，连接 $AC$，则 $AC$ 与 $AB$，$BC$ 构成直角三角形，根据勾股定理得，则 $AC = \sqrt{AB^{2}+BC^{2}} = \sqrt{1^{2}+2^{2}} = \sqrt{5} \approx 2.236$，$\because 2.2$ cm $＜ 2.236$ cm，$\therefore$ 该长方形能从内框内通过（将该长方形的宽沿着 $AC$ 斜着进去）；
(2) 能，理由是：过点 $C$ 作 $CD \perp AB$，则 $\triangle ACD$ 是等腰直角三角形，即 $AD = CD$，$\because AC = \sqrt{2}$，$\therefore CD^{2}+AD^{2}=AC^{2}$，$2CD^{2}=(\sqrt{2})^{2}$，$\because CD^{2}=1$，$CD = 1 ＜ 1.05$，这个立柜能通过过道.

13. (2025春·瑶海区期中)与危险相伴,与烈火为伍,致敬和平年代的英雄,最美的逆行者——中国消防员.云梯消防车是常见的消防器械,云梯最多能伸长到30米,消防车高3米,如图,某栋楼发生火灾,在这栋楼的B处有一老人需要救援,救人时消防车上的云梯伸长至最长,此时消防车的位置A与楼房的距离为24米.
(1)求B处与地面的距离;21米
(2)完成B处的救援后,消防员发现在B处的上方6米的D处有一小孩没有及时撤离,为了能成功地救出小孩,则消防车从A处向着火的楼房靠近的距离AC为多少米?6米

答案：
(1) 在 $Rt\triangle OAB$ 中，$\because AB = 30$ 米，$OA = 24$ 米，$OE = 3$ 米，$\therefore OB = \sqrt{AB^{2}-OA^{2}} = \sqrt{30^{2}-24^{2}} = 18$（米），$\therefore BE = OB + OE = 18 + 3 = 21$（米），答：$B$ 处与地面的距离是 21 米；
(2) 由题意得 $BD = 6$ 米，$\because CD = 30$ 米，$OD = OB + BD = 18 + 6 = 24$（米），$\therefore OC = \sqrt{CD^{2}-OD^{2}} = \sqrt{30^{2}-24^{2}} = 18$（米），$\therefore AC = OA - OC = 24 - 18 = 6$（米）. 答：消防车从 $A$ 处向着火的楼房靠近的距离 $AC$ 为 6 米.

14. (2023春·商河县期末)如图,在△ABC中,∠C=90°,点P在AC上运动,点D在AB上运动,PD始终保持与PA相等,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)判断DE与PD的位置关系,并说明理由;
(2)若AC=3,BC=4,PA=1,求线段DE的长.
(1) DE与PD的位置关系是DE⊥DP，理由如下：∵PD=PA，∴∠A=∠PDA. ∵EF是BD的垂直平分线，∴EB=ED，∴∠B=∠EDB. ∵∠C=90°，∴∠A+∠B=90°，∴∠PDA+∠EDB=90°，∴∠PDE=180°-90°=90°，∴DE⊥DP；
(2) 线段DE的长为19/8.

答案：
(1) $DE \perp DP$，理由如下：$\because PD = PA$，$\therefore \angle A = \angle PDA$. $\because EF$ 是 $BD$ 的垂直平分线，$\therefore EB = ED$，$\therefore \angle B = \angle EDB$. $\because \angle C = 90^{\circ}$，$\therefore \angle A + \angle B = 90^{\circ}$，$\therefore \angle PDA + \angle EDB = 90^{\circ}$，$\therefore \angle PDE = 180^{\circ} - 90^{\circ} = 90^{\circ}$，$\therefore DE \perp DP$；
(2) 连接 $PE$，设 $DE = x$，则 $EB = ED = x$，$CE = 4 - x$. $\because \angle C = \angle PDE = 90^{\circ}$，$\therefore PC^{2}+CE^{2}=PE^{2}=PD^{2}+DE^{2}$，$\therefore 2^{2}+(4 - x)^{2}=1^{2}+x^{2}$，解得：$x = \frac{19}{8}$，则 $DE = \frac{19}{8}$.