第88页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
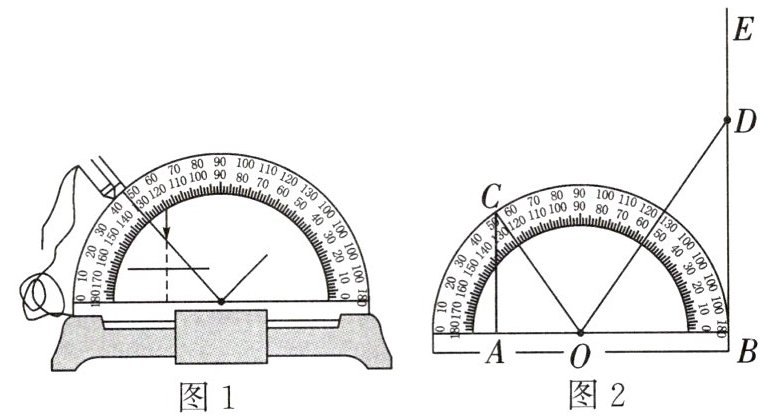
6. (2025春·甘井子区阶段考)小丽在物理实验课上利用如图1所示"光的反射演示器"直观呈现了光的反射原理.如图2,她用激光笔从量角器左边边缘点C处发出光线,经量角器圆心O处(此处放置平面镜)反射后,反射光线落在右边光屏BE上的点D处(B也在量角器的边缘上,O为量角器的中心,A,O,B三点共线,$CA\perp AB$,$BE\perp AB$).小丽在实验中还记录下了$AC=8cm$,$AB=16cm$.依据记录的数据,求量角器的半径OB长.

答案:
$\because CA⊥AB$,$\therefore ∠CAO=90^{\circ}$,设$OB=OC=xcm$,$\because AB=16cm$,$\therefore AO=AB-OB=(16-x)cm$,在$Rt\triangle ACO$中,$AC=8cm$,$AC^{2}+OA^{2}=OC^{2}$,$\therefore 8^{2}+(16-x)^{2}=x^{2}$,解得:$x=10$,$\therefore OB=OC=10cm$,$\therefore$量角器的半径$OB$长为10cm.
$\because CA⊥AB$,$\therefore ∠CAO=90^{\circ}$,设$OB=OC=xcm$,$\because AB=16cm$,$\therefore AO=AB-OB=(16-x)cm$,在$Rt\triangle ACO$中,$AC=8cm$,$AC^{2}+OA^{2}=OC^{2}$,$\therefore 8^{2}+(16-x)^{2}=x^{2}$,解得:$x=10$,$\therefore OB=OC=10cm$,$\therefore$量角器的半径$OB$长为10cm.

7. (2025春·荔湾区期中)周末,数学兴趣小组来到广场做活动课题,并制作如下实践报告:
|活动课题|风筝离地面垂直高度的探究|
|----|----|
|问题背景|风筝由中国古代劳动人民发明于东周春秋时期,距今已2000多年,相传墨翟以木头制成木鸟,研制三年而成,是人类最早的风筝起源.|
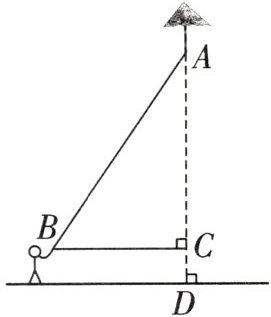
|测量数据|假设风筝放飞时风筝线在空中被拉直(线段AB).勘测组测量了相关数据,并画出如图的示意图,测得人放风筝的手与风筝的水平距离BC的长为15米,风筝线AB的长为25米,牵线放风筝的手到地面的距离为1.7米.|
数据处理组得到数据以后做了认真分析,请帮助他们完成以下任务:
(1)根据测量所得数据,计算出风筝离地面的垂直高度AD;
(2)如果风筝沿AD方向下降了12米,BC的长度保持不变,求要回收多少米的风筝线?
|活动课题|风筝离地面垂直高度的探究|
|----|----|
|问题背景|风筝由中国古代劳动人民发明于东周春秋时期,距今已2000多年,相传墨翟以木头制成木鸟,研制三年而成,是人类最早的风筝起源.|
|测量数据|假设风筝放飞时风筝线在空中被拉直(线段AB).勘测组测量了相关数据,并画出如图的示意图,测得人放风筝的手与风筝的水平距离BC的长为15米,风筝线AB的长为25米,牵线放风筝的手到地面的距离为1.7米.|
数据处理组得到数据以后做了认真分析,请帮助他们完成以下任务:
(1)根据测量所得数据,计算出风筝离地面的垂直高度AD;
(2)如果风筝沿AD方向下降了12米,BC的长度保持不变,求要回收多少米的风筝线?

答案:
(1)由题意得,$∠ACB=90^{\circ}$,$BC=15$米,$AB=25$米,在$Rt\triangle ABC$中,由勾股定理得,$AC^{2}=AB^{2}-BC^{2}$,$\therefore AC=\sqrt{25^{2}-15^{2}}=20$(米),则$AD=AC+CD=21.7$米;
(2)如图,当风筝沿$AD$方向下降了12米时,$\therefore A'C=AC-A'A=20-12=8$(米),在$Rt\triangle A'BC$中,由勾股定理得,$A'B^{2}=A'C^{2}+BC^{2}$,$\therefore A'B=\sqrt{8^{2}+15^{2}}=17$(米),$\therefore 25-17=8$(米),$\therefore$要回收8米的风筝线.
(1)由题意得,$∠ACB=90^{\circ}$,$BC=15$米,$AB=25$米,在$Rt\triangle ABC$中,由勾股定理得,$AC^{2}=AB^{2}-BC^{2}$,$\therefore AC=\sqrt{25^{2}-15^{2}}=20$(米),则$AD=AC+CD=21.7$米;
(2)如图,当风筝沿$AD$方向下降了12米时,$\therefore A'C=AC-A'A=20-12=8$(米),在$Rt\triangle A'BC$中,由勾股定理得,$A'B^{2}=A'C^{2}+BC^{2}$,$\therefore A'B=\sqrt{8^{2}+15^{2}}=17$(米),$\therefore 25-17=8$(米),$\therefore$要回收8米的风筝线.

查看更多完整答案,请扫码查看


