《2025年高效精练八年级数学上册苏科版》

9. 如图,在 $ 5 × 8 $ 的方格纸中,仅用直尺你能分别画出图中线段 $ AB $,$ CD $ 的垂直平分线吗? 试试看.

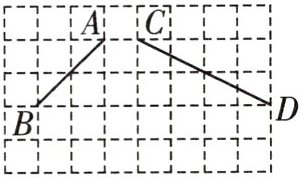
能画出。具体画法为：利用方格纸的格点特征，通过找中点（数方格横向、纵向格点数的中间位置）以及构造到线段两端点距离相等的点（利用勾股定理在方格中构造全等直角三角形或满足$a^{2}+b^{2}=c^{2}$的点），再过中点作与线段垂直的直线（利用方格的直角），从而画出$AB$、$CD$的垂直平分线。

答案： 【解析】：
- 对于线段$AB$：
利用方格纸的特点，找到$AB$的横向格点数为$2$，纵向格点数为$2$。
分别以$A$、$B$为起点，向右下方和左上方平移，找到到$A$、$B$距离相等的点（利用勾股定理，在方格中构造全等的直角三角形）。
设$A$点坐标$(x_1,y_1)$，$B$点坐标$(x_2,y_2)$，通过数方格可知，$AB$的中点可以通过横向和纵向格点数的一半来确定（在方格中直观体现），然后过中点作与$AB$垂直的直线（利用方格的直角特性）。
对于线段$CD$：
同样观察$CD$在方格中的格点情况，$CD$横向格点数为$3$，纵向格点数为$1$。
利用方格构造到$C$、$D$距离相等的点（根据勾股定理$a^{2}+b^{2}=c^{2}$，在方格中找满足条件的点）。
先确定$CD$中点（通过数方格的横向和纵向格点数的中间位置），再根据方格的直角画出垂直平分线（垂直的判定：若两直线相交成直角，则两直线垂直，在方格中利用边与边的关系体现）。
【答案】：能画出。具体画法为：利用方格纸的格点特征，通过找中点（数方格横向、纵向格点数的中间位置）以及构造到线段两端点距离相等的点（利用勾股定理在方格中构造全等直角三角形或满足$a^{2}+b^{2}=c^{2}$的点），再过中点作与线段垂直的直线（利用方格的直角），从而画出$AB$、$CD$的垂直平分线。

10. (2024秋·谷城县期末)如图,$ AD $ 与 $ BC $ 相交于点 $ O $,$ OA = OC $,$ \angle A = \angle C $,$ BE = DE $. 求证:$ OE $ 垂直平分 $ BD $.

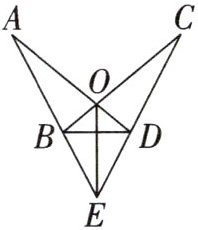
证明: 在 △AOB 与 △COD 中, $\begin{cases} ∠A = ∠C, \\ OA = OC, \\ ∠AOB = ∠COD, \end{cases}$ ∴ △AOB ≌ △COD (ASA), ∴ OB = OD, ∴ 点 O 在线段 BD 的垂直平分线上. ∵ BE = DE, ∴ 点 E 在线段 BD 的垂直平分线上, ∴ OE 垂直平分 BD.

答案： 证明: 在 △AOB 与 △COD 中, $\begin{cases} ∠A = ∠C, \\ OA = OC, \\ ∠AOB = ∠COD, \end{cases}$
∴ △AOB ≌ △COD (ASA),
∴ OB = OD,
∴ 点 O 在线段 BD 的垂直平分线上.
∵ BE = DE,
∴ 点 E 在线段 BD 的垂直平分线上,
∴ OE 垂直平分 BD.

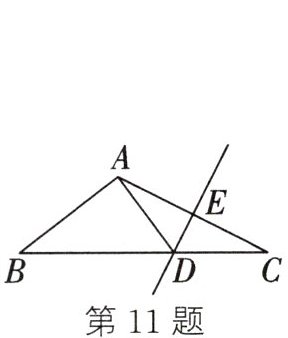
11. (2024秋·红河县期末)如图,在 $ \triangle ABC $ 中,$ DE $ 是 $ AC $ 的垂直平分线,$ AC = 8 \text{ cm} $,且 $ \triangle ABD $ 的周长为 $ 14 \text{ cm} $,则 $ \triangle ABC $ 的周长为 (C)

A. $ 15 \text{ cm} $
B. $ 18 \text{ cm} $
C. $ 22 \text{ cm} $
D. $ 25 \text{ cm} $

答案： C

12. (2024秋·滨城区期末)如图是一风筝的骨架图,点 $ E $ 是 $ BD $ 中点,且 $ AC $ 垂直于 $ BD $,若 $ AB = 2 \text{ cm} $,四边形 $ ABCD $ 的周长为 $ 16 \text{ cm} $,则 $ CD $ 的长为 (B)

A. $ 2 \text{ cm} $
B. $ 6 \text{ cm} $
C. $ 7 \text{ cm} $
D. $ 14 \text{ cm} $

答案： B

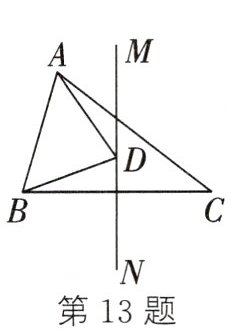
13. (2024秋·交城县期末)如图,在 $ \triangle ABC $ 中,$ AB = 5 $,$ BC = 10 $,$ AC = 9 $,$ MN $ 为边 $ BC $ 的垂直平分线,点 $ D $ 为直线 $ MN $ 上一动点,则 $ \triangle ABD $ 的周长的最小值为 (C)

A. 10
B. 12
C. 14
D. 15

答案： C

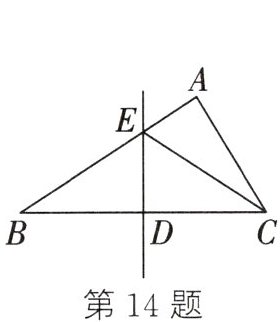
14. (2024秋·隆回县期末)如图,在 $ \triangle ABC $ 中,$ BC $ 的垂直平分线交 $ AB $,$ BC $ 于点 $ E $,$ D $,$ CD = 5 $,$ \triangle BCE $ 的周长为 $ 24 $,则 $ BE = $______7.

答案： 7