《2025年高效精练八年级数学上册苏科版》

14. 如图,在四边形ABCD中,$AB=CB,AD=CD$.你能说明$∠C=∠A$吗? 试一试.

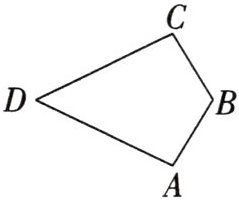
连接 $ B D $, 在 $ \triangle A B D $ 和 $ \triangle C B D $ 中, $ \because A B = C B, A D = C D $, $ B D = B D, \therefore \triangle A B D \cong \triangle C B D, \therefore \angle C = \angle A $.

答案： 连接 $ B D $, 在 $ \triangle A B D $ 和 $ \triangle C B D $ 中, $ \because A B = C B, A D = C D $, $ B D = B D, \therefore \triangle A B D \cong \triangle C B D, \therefore \angle C = \angle A $.

15. (2024秋·番禺区期末)在$△ABC$与$△A'B'C'$中,边BC与边$B'C'$上的中线分别为AD与$A'D'$.若$AB=A'B',BC=B'C',AD=A'D'$.求证:$△ABC\cong △A'B'C'$.



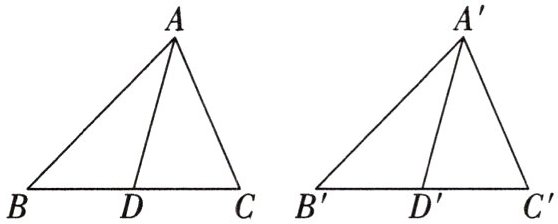
证明: $ \because A D, A ^ { \prime } D ^ { \prime } $ 分别是 $ \triangle A B C, \triangle A ^ { \prime } B ^ { \prime } C ^ { \prime } $ 的中线, $ B C = B ^ { \prime } C ^ { \prime }, \therefore B D = \frac { 1 } { 2 } B C, B ^ { \prime } D ^ { \prime } = \frac { 1 } { 2 } B ^ { \prime } C ^ { \prime } $, $ \therefore B D = B ^ { \prime } D ^ { \prime } $, 在 $ \triangle A B D $ 和 $ \triangle A ^ { \prime } B ^ { \prime } D ^ { \prime } $ 中, $ \left\{ \begin{array} { l } { A B = A ^ { \prime } B ^ { \prime }, } \\ { A D = A ^ { \prime } D ^ { \prime }, } \\ { B D = B ^ { \prime } D ^ { \prime }, } \end{array} \right. $ $ \therefore \triangle A B D \cong \triangle A ^ { \prime } B ^ { \prime } D ^ { \prime } $(SSS),$ \therefore \angle B = \angle B ^ { \prime } $, 在 $ \triangle A B C $ 和 $ \triangle A ^ { \prime } B ^ { \prime } C ^ { \prime } $ 中, $ \left\{ \begin{array} { l } { A B = A ^ { \prime } B ^ { \prime }, } \\ { \angle B = \angle B ^ { \prime }, } \\ { B C = B ^ { \prime } C ^ { \prime }, } \end{array} \right. $ $ \therefore \triangle A B C \cong \triangle A ^ { \prime } B ^ { \prime } C ^ { \prime } $(SAS).

答案： 证明: $ \because A D, A ^ { \prime } D ^ { \prime } $ 分别是 $ \triangle A B C, \triangle A ^ { \prime } B ^ { \prime } C ^ { \prime } $ 的中线, $ B C = B ^ { \prime } C ^ { \prime }, \therefore B D = \frac { 1 } { 2 } B C, B ^ { \prime } D ^ { \prime } = \frac { 1 } { 2 } B ^ { \prime } C ^ { \prime } $, $ \therefore B D = B ^ { \prime } D ^ { \prime } $, 在 $ \triangle A B D $ 和 $ \triangle A ^ { \prime } B ^ { \prime } D ^ { \prime } $ 中, $ \left\{ \begin{array} { l } { A B = A ^ { \prime } B ^ { \prime }, } \\ { A D = A ^ { \prime } D ^ { \prime }, } \\ { B D = B ^ { \prime } D ^ { \prime }, } \end{array} \right. $ $ \therefore \triangle A B D \cong \triangle A ^ { \prime } B ^ { \prime } D ^ { \prime } ( S S S ), \therefore \angle B = \angle B ^ { \prime } $, 在 $ \triangle A B C $ 和 $ \triangle A ^ { \prime } B ^ { \prime } C ^ { \prime } $ 中, $ \left\{ \begin{array} { l } { A B = A ^ { \prime } B ^ { \prime }, } \\ { \angle B = \angle B ^ { \prime }, } \\ { B C = B ^ { \prime } C ^ { \prime }, } \end{array} \right. $ $ \therefore \triangle A B C \cong \triangle A ^ { \prime } B ^ { \prime } C ^ { \prime } ( S A S ) $.

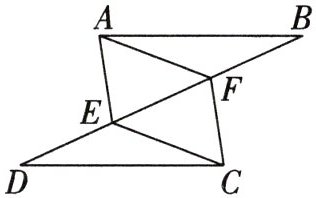
16. (2024·淄博)如图,已知$AB=CD$,点E,F在线段BD上,且$AF=CE$.
请从①$BF=DE$;②$∠BAF=∠DCE$;③$AF=CF$中.选择一个合适的选项作为已知条件,使得$△ABF\cong △CDE$.
你添加的条件是:______① (或②)(只填写一个序号).
添加条件后,请证明$AE// CF$.

答案： 当选择① $ B F = D E $ 时, $ \triangle A B F \cong \triangle C D E $, 证明如下: 在 $ \triangle A B F $ 和 $ \triangle C D E $ 中, $ \left\{ \begin{array} { l } { A B = C D, } \\ { A F = C E, } \\ { B F = D E, } \end{array} \right. $ $ \therefore \triangle A B F \cong \triangle C D E ( S S S ) $, $ \therefore \angle B = \angle D, B F = D E, \therefore B F + E F = D E + E F $, 即 $ B E = D F $, 在 $ \triangle A B E $ 和 $ \triangle C D F $ 中, $ \left\{ \begin{array} { l } { A B = C D, } \\ { \angle B = \angle D, } \\ { B E = D F, } \end{array} \right. $ $ \therefore \triangle A B E \cong \triangle C D F ( S A S ), \therefore \angle A E B = \angle C F D $, $ \therefore A E // C F $; 当选择② $ \angle B A F = \angle D C E $ 时, $ \triangle A B F \cong \triangle C D E $, 证明如下: 在 $ \triangle A B F $ 和 $ \triangle C D E $ 中, $ \left\{ \begin{array} { l } { A B = C D, } \\ { \angle B A F = \angle D C E, } \\ { A F = C E, } \end{array} \right. $ $ \therefore \triangle A B F \cong \triangle C D E ( S A S ) $; $ \therefore \angle B = \angle D, B F = D E $, 同理可证: $ \triangle A B E \cong \triangle C D F ( S A S ), \therefore \angle A E B = \angle C F D, \therefore A E // C F $; 当选择③ $ A F = C F $ 时, 不能判定 $ \triangle A B F \cong \triangle C D E $, 故答案为: ① (或②).