《2025年全效学习学业评价方案八年级数学上册华师大版》

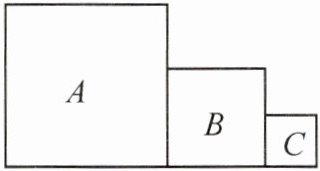
8. [2024·深圳]如图，$A$、$B$、$C$ 均为正方形，若 $A$ 的面积为 $10$，$C$ 的面积为 $1$，则 $B$ 的边长可以是8.2.（写出一个答案即可）

答案： 8.2(答案不唯一)

9. 计算：
(1)$\sqrt{81}-\sqrt[3]{125}$；
(2)$\sqrt{9}-\sqrt{(-6)^2}-\sqrt[3]{-27}$；
(3)$\sqrt[3]{8}+\sqrt{0}-\sqrt{\dfrac{1}{4}}+\sqrt[3]{-\dfrac{1}{8}}$.

答案： 9.
(1)4
(2)0
(3)1

10. 如图，点 $A$ 是数轴上表示实数 $a$ 的点.
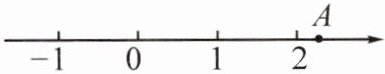
(1)用直尺和圆规在数轴上作出表示实数 $\sqrt{2}$ 的点 $P$；（保留作图痕迹，不写作法）
(2)利用数轴比较 $\sqrt{2}$ 和 $a$ 的大小，并说明理由.

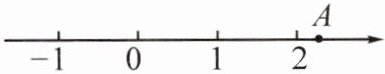
答案：
10.
解:
(1)
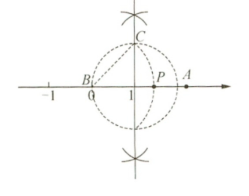
$(2)a＞\sqrt{2},理由如下:$
$如图所示,点A在点P的右侧$
$∴a＞\sqrt{2}$

11.（应用意识）[2023 春·白城期中]如图，一只蚂蚁从点 $A$ 沿数轴向右爬行 $2$ 个单位长度到达点 $B$，点 $A$ 表示的数为 $-\sqrt{2}$，设点 $B$ 表示的数为 $m$.
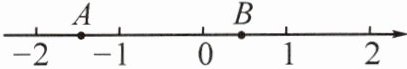
(1)实数 $m$ 的值是$2-\sqrt{2}$；
(2)求 $\vert m + 1\vert + \vert m - 1\vert$ 的值；
|m+1|+|m-1|的值为2.
(3)在数轴上还有 $C$、$D$ 两点分别表示实数 $c$ 和 $d$，且有 $\vert 2c + d\vert$ 与 $\sqrt{d^2 - 16}$ 互为相反数，求 $2c - 3d$ 的平方根.
2c-3d的平方根为$\pm4.$

答案： $11.(1)2-\sqrt{2} (2)$|m+1|+|m-1|的值为2.
(3)2c-3d的平方根为$\pm4.$