第38页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
8. [2024 春·眉山月考]先化简,再求值:$(a - 2b)^{2} + (b - 3a)(b + 3a) - 2(a - 4b)(a + b)$,其中 $a = - 1$,$b = \frac{1}{2}$。
答案:
8. 原式$=-10a^{2}+2ab + 13b^{2},$当$a=-1,b=\frac{1}{2}$时,原式$=-\frac{31}{4}.$
9. 小丽和小兵在计算 $(2x + 5)(2x - 5) + 2(4x + 3) - 4(x + 1)^{2}$ 并求值时,他们进行了如下的对话。小丽说:“我发现这个式子,当 $x = 2024$ 和 $x = 2025$ 时,它的值始终是相等的。”小兵说:“不可能,对于不同的 $x$ 的值,应该有不同的结果。”你认为谁说得对呢?请说明理由。
答案:
9. 小丽说得对.理由略.
10. 阅读理解:
若 $x$ 满足 $(30 - x)(x - 10) = 160$,求 $(30 - x)^{2} + (x - 10)^{2}$ 的值。
解:设 $30 - x = a$,$x - 10 = b$,
则 $(30 - x)(x - 10) = ab = 160$,$a + b = (30 - x) + (x - 10) = 20$,$(30 - x)^{2} + (x - 10)^{2} = a^{2} + b^{2} = (a + b)^{2} - 2ab = 20^{2} - 2×160 = 80$。
解决问题:
(1)若 $x$ 满足 $(2027 - x)^{2} + (x - 2024)^{2} = 2026$,求 $(2027 - x)(x - 2024)$ 的值。
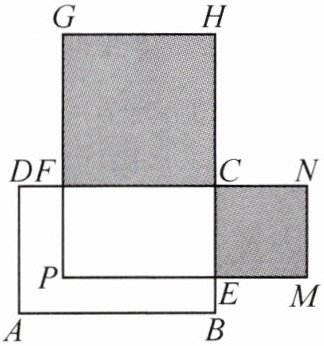
(2)如图,在长方形 $ABCD$ 中,$AB = 20$,$BC = 12$,点 $E$、$F$ 是 $BC$、$CD$ 上的点,且 $BE = DF = x$。分别以 $FC$、$CE$ 为边在长方形 $ABCD$ 外侧作正方形 $CFGH$ 和 $CEMN$。若长方形 $CEPF$ 的面积为 $160$,求图中阴影部分的面积和。
若 $x$ 满足 $(30 - x)(x - 10) = 160$,求 $(30 - x)^{2} + (x - 10)^{2}$ 的值。
解:设 $30 - x = a$,$x - 10 = b$,
则 $(30 - x)(x - 10) = ab = 160$,$a + b = (30 - x) + (x - 10) = 20$,$(30 - x)^{2} + (x - 10)^{2} = a^{2} + b^{2} = (a + b)^{2} - 2ab = 20^{2} - 2×160 = 80$。
解决问题:
(1)若 $x$ 满足 $(2027 - x)^{2} + (x - 2024)^{2} = 2026$,求 $(2027 - x)(x - 2024)$ 的值。
(2)如图,在长方形 $ABCD$ 中,$AB = 20$,$BC = 12$,点 $E$、$F$ 是 $BC$、$CD$ 上的点,且 $BE = DF = x$。分别以 $FC$、$CE$ 为边在长方形 $ABCD$ 外侧作正方形 $CFGH$ 和 $CEMN$。若长方形 $CEPF$ 的面积为 $160$,求图中阴影部分的面积和。

答案:
$10. (1)-\frac{2017}{2} (2)$阴影部分的面积和为384.
查看更多完整答案,请扫码查看


