第59页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
2. [2024·内江期末]下列命题是真命题的是(
A.相等的角是对顶角
B.若数a、b满足a² = b²,则a = b
C.垂直于同一条直线的两条直线互相平行
D.垂线段最短
D
)A.相等的角是对顶角
B.若数a、b满足a² = b²,则a = b
C.垂直于同一条直线的两条直线互相平行
D.垂线段最短
答案:
2.D
1. [2024秋·眉山期末]下列命题是真命题的是(
A.内错角相等
B.三角形内角和是180°
C.√6是有理数
D.若|a| = 1,则a = 1
B
)A.内错角相等
B.三角形内角和是180°
C.√6是有理数
D.若|a| = 1,则a = 1
答案:
1.B
2. [2024秋·宜宾期中]对于命题“如果x为任意实数,那么√x² = x”,能说明它是假命题的反例是(
A.x = 0
B.x = 3
C.x = 0.5
D.x = -1
D
)A.x = 0
B.x = 3
C.x = 0.5
D.x = -1
答案:
2.D
3. 把下列命题改写成“如果……,那么……”的形式,并指出其条件和结论。
(1)等角的余角相等;
(2)小于直角的角是锐角;
(3)两点确定一条直线。
(1)等角的余角相等;
(2)小于直角的角是锐角;
(3)两点确定一条直线。
答案:
3.
(1)如果两个角相等,那么它们的余角也相等.条件是“两个角相等”,结论是“它们的余角也相等”.
(2)如果一个角小于直角,那么这个角是锐角.条件是“一个角小于直角”,结论是“这个角是锐角”.
(3)如果过已知两点画直线,那么能且只能画一条直线.条件是“过已知两点画直线”,结论是“能且只能画一条直线”.
(1)如果两个角相等,那么它们的余角也相等.条件是“两个角相等”,结论是“它们的余角也相等”.
(2)如果一个角小于直角,那么这个角是锐角.条件是“一个角小于直角”,结论是“这个角是锐角”.
(3)如果过已知两点画直线,那么能且只能画一条直线.条件是“过已知两点画直线”,结论是“能且只能画一条直线”.
4. 判断下列命题是真命题,还是假命题。如果是假命题,请举一个反例。
(1)若a² > b²,则a > b;
(2)同位角相等,两直线平行;
(3)一个角的余角小于这个角;
(4)一个钝角与一个锐角的和必为一个平角;
(5)两直线被第三条直线所截,同旁内角互补;
(6)如果n是自然数,那么n² + n + 17是质数。
(1)若a² > b²,则a > b;
(2)同位角相等,两直线平行;
(3)一个角的余角小于这个角;
(4)一个钝角与一个锐角的和必为一个平角;
(5)两直线被第三条直线所截,同旁内角互补;
(6)如果n是自然数,那么n² + n + 17是质数。
答案:
4.
(1)假命题.反例:a=-3,b=0,
∵9>0,即$ a^{2}>b^{2},$但是 -3<0,即 a<b.
(2)真命题.
(3)假命题.反例:若∠α=20°,则∠α的余角为70°,70°>20°,此时∠α的余角大于∠α.
(4)假命题.反例:100°+30°=130°<180°,此时钝角100°与锐角30°的和不为平角.
(5)假命题.反例:在任意三角形中,其中两边所在直线被第三边所在直线所截,此时的同旁内角为三角形两内角,显然不互补.
(6)假命题.反例:n=17时,此数为合数.
(1)假命题.反例:a=-3,b=0,
∵9>0,即$ a^{2}>b^{2},$但是 -3<0,即 a<b.
(2)真命题.
(3)假命题.反例:若∠α=20°,则∠α的余角为70°,70°>20°,此时∠α的余角大于∠α.
(4)假命题.反例:100°+30°=130°<180°,此时钝角100°与锐角30°的和不为平角.
(5)假命题.反例:在任意三角形中,其中两边所在直线被第三边所在直线所截,此时的同旁内角为三角形两内角,显然不互补.
(6)假命题.反例:n=17时,此数为合数.
5. (推理能力)[2023春·顺庆区月考]已知∠ABC的两边与∠DEF的两边分别平行,即AB // DE,BC // EF,试探究:
(1)如图1,∠B与∠E的数量关系是
(2)如图2,写出∠B与∠E的数量关系,并说明理由;
(3)根据上述探究,请归纳概括出一个真命题。

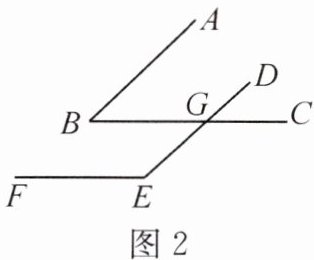
(1)如图1,∠B与∠E的数量关系是
∠B=∠E
;(2)如图2,写出∠B与∠E的数量关系,并说明理由;
(3)根据上述探究,请归纳概括出一个真命题。


答案:
5.
(1)∠B=∠E
(2)∠B+∠E=180°.理由略.
(3)归纳:如果两个角的两边分别平行,那么这两个角相等或互补.
(1)∠B=∠E
(2)∠B+∠E=180°.理由略.
(3)归纳:如果两个角的两边分别平行,那么这两个角相等或互补.
查看更多完整答案,请扫码查看


