第60页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
1. 定义、基本事实、定理与证明
定 义:用不同的语句来说明某些名词各自所包含的
基本事实:一个命题的正确性是人们在长期实践中总结出来的,并把它作为判断其他命题真假的原始依据,这样的命题视为基本事实。
定 理:如果一个命题可以从基本事实或其他真命题出发,用逻辑推理的方法判断它是正确的,并且可以作为进一步判断其他命题真假的依据,这样的
证 明:根据
定 义:用不同的语句来说明某些名词各自所包含的
确切意义
,这样的语句叫做这些名词的定义。基本事实:一个命题的正确性是人们在长期实践中总结出来的,并把它作为判断其他命题真假的原始依据,这样的命题视为基本事实。
定 理:如果一个命题可以从基本事实或其他真命题出发,用逻辑推理的方法判断它是正确的,并且可以作为进一步判断其他命题真假的依据,这样的
真命题
叫做定理。证 明:根据
条件
、定义
及基本事实
、定理
等,经过演绎推理,来判断一个命题是否正确,这样的推理过程叫做证明。
答案:
1.确切意义 真命题 条件 定义 基本事实 定理
例 1 在证明“三角形内角和等于 $180^{\circ}$”这一命题时,小彬的思路如下。请写出“求证”部分,补充第一步推理的依据并按他的思路完成后续证明。
已知:如图,$\triangle ABC$。
求证:
证明:如图,在 $BC$ 边上取点 $D$,过点 $D$ 分别作 $DE // AB$ 交 $AC$ 于点 $E$,$DF // AC$ 交 $AB$ 于点 $F$。
$\because DE // AB$,
$\therefore \angle A = \angle 1$,$\angle B = \angle 2$(依据:
$\because DF // AC$,
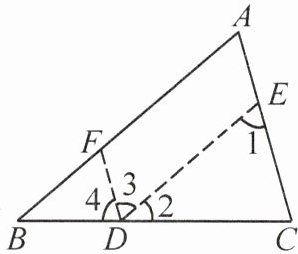
已知:如图,$\triangle ABC$。
求证:
∠A + ∠B + ∠C = 180°
。证明:如图,在 $BC$ 边上取点 $D$,过点 $D$ 分别作 $DE // AB$ 交 $AC$ 于点 $E$,$DF // AC$ 交 $AB$ 于点 $F$。
$\because DE // AB$,
$\therefore \angle A = \angle 1$,$\angle B = \angle 2$(依据:
两直线平行,同位角相等
)。$\because DF // AC$,

补全证明略
答案:
【例1】 ∠A + ∠B + ∠C = 180° 两直线平行,同位角相等 补全证明略
例 2 求证:如果一条直线与两条平行线中的一条垂直,那么这条直线也和另一条直线垂直。(画出图形,写出已知、求证并完成证明)
【点悟】(1)初学几何证明时,要把依据写在每一步推理后面的括号里,这样做的目的是训练在证明推理时,每一步都要有理有据,万万不可随意推测和想当然;(2)证明中的依据一般只限于四种:①题设;②定义;③基本事实;④定理。
【点悟】(1)初学几何证明时,要把依据写在每一步推理后面的括号里,这样做的目的是训练在证明推理时,每一步都要有理有据,万万不可随意推测和想当然;(2)证明中的依据一般只限于四种:①题设;②定义;③基本事实;④定理。
答案:
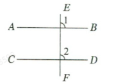
答案已知$:$如图$,AB//CD,AB⊥EF.$求证$:CD⊥EF.$

证明因为$AB//CD($已知$).$
所以$∠1=∠2($两条直线平行,同位角相等$),$
因为$EF⊥AB($已知$),$
所以$∠1=90°($垂直的定义$),$
所以$∠2=90°($等量代换$).$
所以$EF⊥CD($垂直的定义$).$
查看更多完整答案,请扫码查看


