《2025年全效学习学业评价方案八年级数学上册华师大版》

1. 计算$(-2m)^{2}·(-m· m^{2}+3m^{3})$的结果是（A）
A.$8m^{5}$
B.$-8m^{5}$
C.$8m^{6}$
D.$-4m^{4}+12m^{5}$

答案： 1.A

2. 小明回家后，拿出课堂笔记本复习，发现这样一道题：$-3x(-2x^{2}+3x - 1)=6x^{3}-9x^{2}+■$.“■”的地方被墨水弄污了，你认为“■”处应该是（C）
A.$1$
B.$-1$
C.$3x$
D.$-3x$

答案： 2.C

3. [2023·甘肃]计算：$a(a + 2)-2a=$$a^{2}$.

答案： 3.$a^{2}$

4. 计算：
（1）$(-2ab)(3a^{2}-2ab - 4b^{2})$；
（2）$(-\frac{1}{2}m^{2}n-\frac{1}{3}mn + 1)(-\frac{1}{4}m^{3}n)$；
（3）$9x(-2x^{2}-xy + y^{2})(-xy)$.

答案： 4.
(1)$-6a^{3}b + 4a^{2}b^{2}+8ab^{3}$
(2)$\frac{1}{8}m^{5}n^{2}+\frac{1}{12}m^{4}n^{2}-\frac{1}{4}m^{3}n$
(3)$18x^{4}y + 9x^{3}y^{2}-9x^{2}y^{3}$

5. 计算下列棱柱的体积.

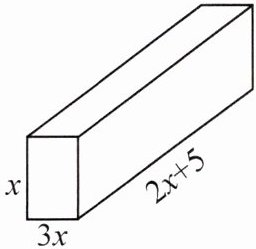
答案： 5.$6x^{3}+15x^{2}$

6. [2024 秋·内江期中]若$a^{2}+3a = 2$，则代数式$5a(a + 3)-2$的值是8.

答案： 6.8

7. [2024·眉山期末]先化简，再求值：$3a(2a^{2}-4a + 3)-2a^{2}(3a + 4)$，其中$a = -2$.

答案： 7.原式$=-20a^{2}+9a$，当$a = -2$时，原式$=-98$.

8. [2024·山西期中]已知$(-2x)·(5 - 3x + mx^{2}-nx^{3})$的计算结果中不含$x^{3}$项，求$m$的值.

答案： 8.$m = 0$

9. 下面是一道例题及其解答过程的一部分，其中$A$是关于$m$的多项式.请写出多项式$A$，并将该例题的解答过程补充完整.
先去括号，再合并同类项：
$m(A)-6(m + 1)$.
解：$m(A)-6(m + 1)$
$=m^{2}+6m-6m - 6$
$=$$m^{2}-6$.
$A$为$m + 6$.

答案： 9.$m^{2}-6$ $A$为$m + 6$.

10. （运算能力）某同学在计算多项式$A$乘$2x^{2}$时，因抄错运算符号，算成了加$2x^{2}$，得到的结果是$x^{2}-4x + 1$，那么正确的计算结果是$-2x^{4}-8x^{3}+2x^{2}$.

答案： 10.$-2x^{4}-8x^{3}+2x^{2}$