第55页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
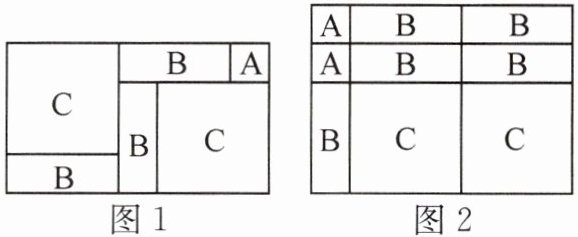
1. 数形结合是解决数学问题的重要思想方法,借助图形可以对很多数学问题进行直观推导和解释。八年级课外活动小组剪了若干个边长为$a$的小正方形($A$类),长为$b$、宽为$a$的长方形($B$类)以及边长为$b$的大正方形($C$类)卡片,发现利用这三种卡片各若干可以拼出一些长方形来解释某些等式。
乐学组的同学:我们拼出了如图1的长方形,发现这个图形可以解释等式:$(a + 2b)(a + b) = a^{2} + 3ab + 2b^{2}$。
(1) 勤奋组的同学拼出了如图2的长方形,这个图形可以解释的等式为____________________________。
(2) 启航组同学要拼成一个长为$(a + 3b)$、宽为$(2a + b)$的长方形,那么需用$A$类卡片________张、$B$类卡片________张、$C$类卡片________张。
(3) 卓越组的同学想用$1$张$A$卡片、$5$张$B$卡片、$4$张$C$卡片拼成一个长方形,验证某个等式,请你帮他们画出图形并写出可以解释的等式。
(4) 善思组的同学用$5$张$B$类卡片按图3的方式不重叠地放在长方形内,两个大长方形用阴影表示,设右下角与左上角的阴影部分的面积之差为$M$,$AB = x$,若$M$的值与$x$无关,试探究$a$与$b$的数量关系,并说明理由。

乐学组的同学:我们拼出了如图1的长方形,发现这个图形可以解释等式:$(a + 2b)(a + b) = a^{2} + 3ab + 2b^{2}$。
(1) 勤奋组的同学拼出了如图2的长方形,这个图形可以解释的等式为____________________________。
(2) 启航组同学要拼成一个长为$(a + 3b)$、宽为$(2a + b)$的长方形,那么需用$A$类卡片________张、$B$类卡片________张、$C$类卡片________张。
(3) 卓越组的同学想用$1$张$A$卡片、$5$张$B$卡片、$4$张$C$卡片拼成一个长方形,验证某个等式,请你帮他们画出图形并写出可以解释的等式。
(4) 善思组的同学用$5$张$B$类卡片按图3的方式不重叠地放在长方形内,两个大长方形用阴影表示,设右下角与左上角的阴影部分的面积之差为$M$,$AB = x$,若$M$的值与$x$无关,试探究$a$与$b$的数量关系,并说明理由。


答案:
$1. (1)(2a + b)(2b + a) = 2a^{2} + 5ab + 2b^{2}$
$(2) 2;7;3$
$(3)$等式为$(a + b)(a + 4b) = a^{2} + 5ab + 4b^{2}.$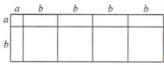 $.$
$.$
$(4)b = 2a,$理由如下$:.$
由题意可得$:M=(x-3a)b-2a(x-b)=xb-3ab-2ax+2ab=(b-2a)x-ab$
∵$M$的值与$x$无关
∴$b-2a=0$
∴$b=2a$
$1. (1)(2a + b)(2b + a) = 2a^{2} + 5ab + 2b^{2}$
$(2) 2;7;3$
$(3)$等式为$(a + b)(a + 4b) = a^{2} + 5ab + 4b^{2}.$
 $.$
$.$ $(4)b = 2a,$理由如下$:.$
由题意可得$:M=(x-3a)b-2a(x-b)=xb-3ab-2ax+2ab=(b-2a)x-ab$
∵$M$的值与$x$无关
∴$b-2a=0$
∴$b=2a$
二、校园实践基地土地分割方案
2. 根据以下素材,探索完成任务。

2. 根据以下素材,探索完成任务。

答案:
任务一:
① $a^{2}+2b^{2}+3ab$;
② $(a+2b)(a + b)$(或$a^{2}+3ab + 2b^{2}$)。
任务二:
$(a + 2b)(a + 3b) = a^{2} + 5ab + 6b^{2}$.
任务三:
由$a^{2}+6b^{2}+5ab = 35$,$a$、$b$为正整数,通过试值法:
当$b = 1$时,$a^{2}+5a+6 = 35$,即$a^{2}+5a - 29 = 0$,$\Delta=25 + 116 = 141$,$a$不是整数。
当$b = 2$时,$a^{2}+10a + 24 = 35$,即$a^{2}+10a - 11 = 0$,$(a + 11)(a - 1)=0$,解得$a = 1$或$a=-11$(舍去)。
所以$a = 1$,$b = 2$($a = 19$(由$a+11 = 19+11 - 35$(通过其他试值不合理舍去)等不合理值舍去) )。
综上,$a = 1$,$b = 2$。
① $a^{2}+2b^{2}+3ab$;
② $(a+2b)(a + b)$(或$a^{2}+3ab + 2b^{2}$)。
任务二:
$(a + 2b)(a + 3b) = a^{2} + 5ab + 6b^{2}$.
任务三:
由$a^{2}+6b^{2}+5ab = 35$,$a$、$b$为正整数,通过试值法:
当$b = 1$时,$a^{2}+5a+6 = 35$,即$a^{2}+5a - 29 = 0$,$\Delta=25 + 116 = 141$,$a$不是整数。
当$b = 2$时,$a^{2}+10a + 24 = 35$,即$a^{2}+10a - 11 = 0$,$(a + 11)(a - 1)=0$,解得$a = 1$或$a=-11$(舍去)。
所以$a = 1$,$b = 2$($a = 19$(由$a+11 = 19+11 - 35$(通过其他试值不合理舍去)等不合理值舍去) )。
综上,$a = 1$,$b = 2$。
查看更多完整答案,请扫码查看


