第107页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
1. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙脚的距离为$0.7m$,顶端距离地面$2.4m$。如果保持梯子底端的位置不动,将梯子斜靠在右墙时,梯子顶端距离地面$2m$,则小巷的宽度为(
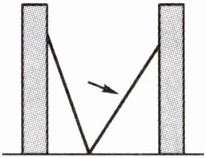
A.$0.7m$
B.$1.5m$
C.$2.2m$
D.$2.4m$
C
)
A.$0.7m$
B.$1.5m$
C.$2.2m$
D.$2.4m$
答案:
1.C
2. 在我国古代数学著作的《九章算术》“勾股”章有一题:今有开门去阃(kǔn)一尺,不合二寸,问门广几何。其意思是:如图,推开双门($AD$和$BC$),门边缘$D$、$C$两点到门槛$AB$的距离为$1$尺($1$尺$=10$寸),双门间的缝隙$CD$为$2$寸,那么门的宽度$AB$(两扇门宽度的和)为(
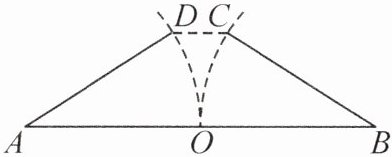
A.$100$寸
B.$101$寸
C.$102$寸
D.$103$寸
B
)
A.$100$寸
B.$101$寸
C.$102$寸
D.$103$寸
答案:
2.B
3. 某楼梯如图所示,欲在楼梯上铺设红色地毯,已知这种地毯每平方米的售价为$30$元,楼梯宽为$2m$,则购买这种地毯至少需要
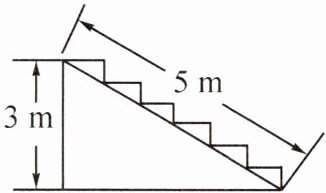
420
元。
答案:
3.420
4. 如图,在树上距地面$10m$的$D$处有两只猴子,它们同时发现地面上$C$处有一筐水果,一只猴子从$D$处向上爬到树顶$A$处,然后利用在$A$处的滑绳$AC$滑到$C$处,另一只猴子从$D$处先滑到地面$B$,再由$B$跑到$C$。已知两只猴子经过的路程都是$15m$,求树高$AB$。
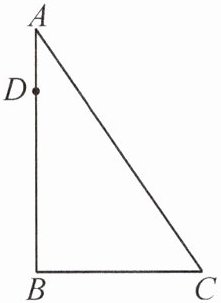

答案:
4.树高AB为12m.
5. (模型观念、应用意识)[2024·陕西]如图,在$6×7$的网格中,每个小正方形的边长均为$1$,$\triangle ABC$和$\triangle DFE$的顶点都在格点上。求证:$\angle ABC=\angle DFE$。
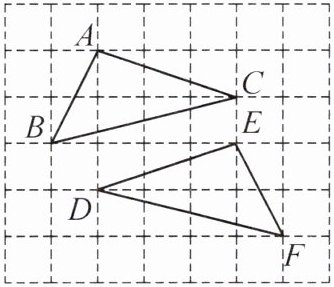

答案:
要证明∠ABC=∠DFE,可通过证明△ABC与△EFD全等实现:
1. 计算△ABC的边长:
由网格知,A与B水平距1,垂直距2,根据勾股定理:$AB=\sqrt{1^2+2^2}=\sqrt{5}$;
B与C水平距3,垂直距1,$BC=\sqrt{3^2+1^2}=\sqrt{10}$;
A与C水平距2,垂直距3,$AC=\sqrt{2^2+3^2}=\sqrt{13}$。
2. 计算△DFE的边长:
F与E水平距1,垂直距2,$FE=\sqrt{1^2+2^2}=\sqrt{5}$;
F与D水平距3,垂直距1,$FD=\sqrt{3^2+1^2}=\sqrt{10}$;
D与E水平距2,垂直距3,$DE=\sqrt{2^2+3^2}=\sqrt{13}$。
3. 证明三角形全等:
在△ABC和△EFD中,
$\because AB=FE=\sqrt{5}$,$BC=FD=\sqrt{10}$,$AC=ED=\sqrt{13}$,
$\therefore \triangle ABC \cong \triangle EFD(SSS)$。
4. 得出角相等结论:
$\therefore \angle ABC=\angle EFD$,即$\angle ABC=\angle DFE$。
结论:$\angle ABC=\angle DFE$。
1. 计算△ABC的边长:
由网格知,A与B水平距1,垂直距2,根据勾股定理:$AB=\sqrt{1^2+2^2}=\sqrt{5}$;
B与C水平距3,垂直距1,$BC=\sqrt{3^2+1^2}=\sqrt{10}$;
A与C水平距2,垂直距3,$AC=\sqrt{2^2+3^2}=\sqrt{13}$。
2. 计算△DFE的边长:
F与E水平距1,垂直距2,$FE=\sqrt{1^2+2^2}=\sqrt{5}$;
F与D水平距3,垂直距1,$FD=\sqrt{3^2+1^2}=\sqrt{10}$;
D与E水平距2,垂直距3,$DE=\sqrt{2^2+3^2}=\sqrt{13}$。
3. 证明三角形全等:
在△ABC和△EFD中,
$\because AB=FE=\sqrt{5}$,$BC=FD=\sqrt{10}$,$AC=ED=\sqrt{13}$,
$\therefore \triangle ABC \cong \triangle EFD(SSS)$。
4. 得出角相等结论:
$\therefore \angle ABC=\angle EFD$,即$\angle ABC=\angle DFE$。
结论:$\angle ABC=\angle DFE$。
查看更多完整答案,请扫码查看


