第43页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
1. 下列计算正确的是(
A.$(a - b)^2 = a^2 - b^2$
B.$(a + 2b)^2 = a^2 + 2ab + 4b^2$
C.$(a^2 + 1)^2 = a^4 + 2a + 1$
D.$(-m - n)^2 = m^2 + 2mn + n^2$
D
)A.$(a - b)^2 = a^2 - b^2$
B.$(a + 2b)^2 = a^2 + 2ab + 4b^2$
C.$(a^2 + 1)^2 = a^4 + 2a + 1$
D.$(-m - n)^2 = m^2 + 2mn + n^2$
答案:
1. D
2. 下列算式能用平方差公式计算的是(
A.$(2a + b)(2b - a)$
B.$(\frac{1}{2} + 1)(-\frac{1}{2} - 1)$
C.$(3x - y)(-3x + y)$
D.$(-m - n)(-m + n)$
D
)A.$(2a + b)(2b - a)$
B.$(\frac{1}{2} + 1)(-\frac{1}{2} - 1)$
C.$(3x - y)(-3x + y)$
D.$(-m - n)(-m + n)$
答案:
2. D
3. 运用完全平方公式计算 $89.8^2$ 的最佳选择是(
A.$(89 + 0.8)^2$
B.$(80 + 9.8)^2$
C.$(90 - 0.2)^2$
D.$(100 - 10.2)^2$
C
)A.$(89 + 0.8)^2$
B.$(80 + 9.8)^2$
C.$(90 - 0.2)^2$
D.$(100 - 10.2)^2$
答案:
3. C
4. [2024 秋·东城区校级期中]若 $a + b = 3$,$ab = -12$,则 $a^2 - ab + b^2$ 的值为(
A.57
B.21
C.45
D.33
C
)A.57
B.21
C.45
D.33
答案:
4. C
5. [2024 秋·如东县期中]在运用乘法公式计算 $(2x - y + 3)(2x + y - 3)$ 时,下列变形正确的是(
A.$[(2x - y) + 3][(2x + y) - 3]$
B.$[(2x - y) + 3][(2x - y) - 3]$
C.$[2x - (y + 3)][2x + (y - 3)]$
D.$[2x - (y - 3)][2x + (y - 3)]$
D
)A.$[(2x - y) + 3][(2x + y) - 3]$
B.$[(2x - y) + 3][(2x - y) - 3]$
C.$[2x - (y + 3)][2x + (y - 3)]$
D.$[2x - (y - 3)][2x + (y - 3)]$
答案:
5. D
6. [2024·礼县模拟]如图,大正方形与小正方形的面积之差是 48,则阴影部分的面积是(
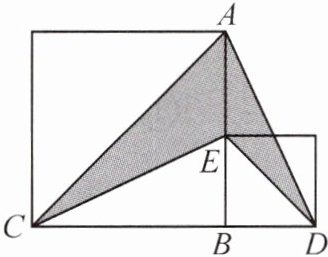
A.12
B.18
C.24
D.30
C
)
A.12
B.18
C.24
D.30
答案:
6. C
7. 计算:
(1) $(-9x^2 + 3x) ÷ (-3x) =$
(2) $x^3 · (2x^3)^2 ÷ (x^4)^2 =$
(1) $(-9x^2 + 3x) ÷ (-3x) =$
3x-1
;(2) $x^3 · (2x^3)^2 ÷ (x^4)^2 =$
4x
。
答案:
7.
(1)3x-1
(2)4x
(1)3x-1
(2)4x
8. [2024 春·福田区期中]若 $(x + 2)^2 = x^2 + kx + 4$,则 $k$ 的值为
4
。
答案:
8. 4
9. 将二次三项式 $x^2 + 4x + 5$ 化成 $(x + p)^2 + q$ 的形式应为
$(x+2)^2+1$
。
答案:
$9. (x+2)^2+1$
10. 已知 $(a + b)^2 = 8$,$(a - b)^2 = 5$,则 $a^2 + b^2 =$
6.5
,$ab =$0.75
。
答案:
10. 6.5 0.75
11. 如图,小颖用 4 张长为 $a$、宽为 $b(a > b)$ 的长方形纸片,按如图的方式拼成一个边长为 $(a + b)$ 的正方形,图中空白部分的面积为 $S_1$,阴影部分的面积为 $S_2$。若 $a = 2b$,则 $S_1$、$S_2$ 之间存在的数量关系是
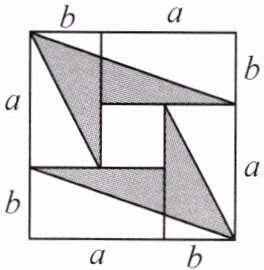
S₁=2S₂
。
答案:
11. S₁=2S₂
查看更多完整答案,请扫码查看


