《2025年同步练习册泰山出版社八年级数学上册青岛版》

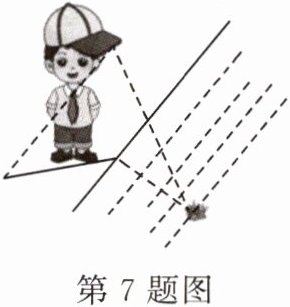
7. 几何学起源于土地测量,据史料记载,古希腊数学家泰勒斯发明了一种用帽子测量河流宽度的方法,具体操作步骤如下：
①如图,人垂直站立在河岸边上,视线与河岸边保持垂直；
②调整帽子,使视线通过帽檐正好落在对面的河岸边；
③人保持姿势,转过一个角度,这时视线通过帽檐落在了自己所在岸的某一点上；
④测量该点与人站立位置的距离就是河流的宽度。
请用你学过的一个数学定理解释通过以上步骤能测得河流宽度的道理：______。

答案： ASA

8. 如图,$ AB = AC $,$ AD = AE $,$ \angle BAC = \angle DAE $,$ \angle 1 = 22° $,$ \angle 2 = 34° $,则 $ \angle 3 = $______。

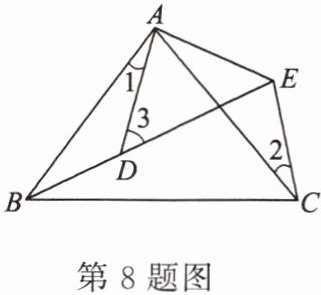
答案： 56°

9. 如图是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线 $ BD $ 上,转轴 $ B $ 到地面的距离 $ BD = 2.5 m $。小乐在荡秋千过程中,当秋千摆动到最高点 $ A $ 时,测得点 $ A $ 到 $ BD $ 的距离 $ AC = 1.5 m $,点 $ A $ 到地面的距离 $ AE = 1.5 m $,当他从 $ A $ 处摆动到 $ A' $ 处时,若 $ A'B \perp AB $,$ A' $ 到 $ BD $ 的距离是______。

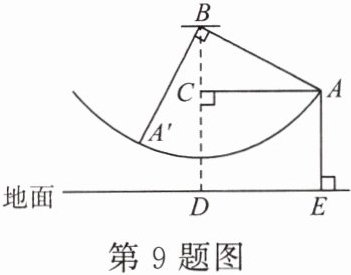
答案： 1 m

10. 如图,$ CA \perp AB $,垂足为 $ A $,$ AB = 8 $,$ AC = 4 $,射线 $ BM \perp AB $,垂足为 $ B $,一动点 $ E $ 从 $ A $ 点出发以 2 每秒的速度沿射线 $ AN $ 运动,点 $ D $ 为射线 $ BM $ 上一动点,随着 $ E $ 点运动而运动,且始终保持 $ ED = CB $,当点 $ E $ 运动______秒时,$ \triangle DEB $ 与 $ \triangle BCA $ 全等。

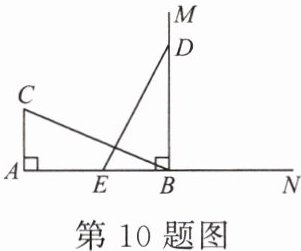
答案： 0,2,6,8

11. (13分)如图,有一池塘,要测量池塘两端 $ A $,$ B $ 的距离,可先在平地上取一个点 $ C $,从点 $ C $ 不经过池塘可以直接到达点 $ A $ 和 $ B $。连接 $ AC $ 并延长到点 $ D $,使 $ CD = CA $。连接 $ BC $ 并延长到点 $ E $,使 $ CE = CB $。连接 $ DE $,那么量出 $ DE $ 的长就是 $ A $,$ B $ 的距离。为什么？

答案： 解：量出 DE 的长就等于 AB 的长。理由：在△ABC 和△DEC 中，$\left\{\begin{array}{l} BC=CE,\\ ∠ACB=∠DCE,\\ CA=CD,\end{array}\right. $所以△ABC≌△DEC(SAS)。所以 AB=DE。