第120页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
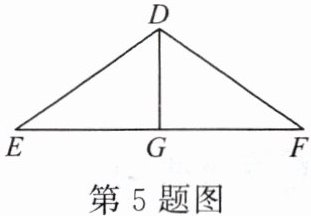
5. 如图,在$\triangle DEF$中,$DE = 17\mathrm{cm},EF = 30\mathrm{cm}$,$EF边上的中线DG的长为8\mathrm{cm}$。求证:$DG\perp EF$。

答案:
证明:因为点G是EF的中点,所以$EG=\frac {1}{2}EF=\frac {1}{2}×30=15(cm)$。因为$DG^{2}+EG^{2}=8^{2}+15^{2}=289=17^{2}=DE^{2},$所以$\triangle DGE$是直角三角形,所以$DG⊥EF$。
6. 为了积极响应国家乡村振兴号召,某镇政府采用了移动宣讲的形式进行宣传动员。如图,笔直公路$MN的一侧点A$处有一村庄,村庄到公路$MN的距离为600\mathrm{m}$,假使宣讲车$P周围1000\mathrm{m}$以内能听到广播宣传,宣讲车$P在公路MN上沿PN$方向行驶时:
(1)判断村庄能否听到宣传,并说明理由;
(2)如果能听到,已知宣讲车的速度是$200\mathrm{m/min}$,那么村庄总共能听到多长时间的宣传?

(1)判断村庄能否听到宣传,并说明理由;
(2)如果能听到,已知宣讲车的速度是$200\mathrm{m/min}$,那么村庄总共能听到多长时间的宣传?

答案:
解:
(1)能听到宣传。理由:因为村庄A到公路MN的距离为600m<1000m,所以村庄能听到宣传。
(2)假设当宣讲车行驶到P点村庄开始能听到宣讲,行驶到Q点村庄恰不能听到宣讲,则$AP=AQ=1000m,AB=600m,$所以$BP=BQ=\sqrt {1000^{2}-600^{2}}=800(m)$。所以$PQ=1600m$。所以村庄能听到宣讲的时间为$1600÷200=8(min)$。所以村庄总共能听到8min的宣传。
(1)能听到宣传。理由:因为村庄A到公路MN的距离为600m<1000m,所以村庄能听到宣传。
(2)假设当宣讲车行驶到P点村庄开始能听到宣讲,行驶到Q点村庄恰不能听到宣讲,则$AP=AQ=1000m,AB=600m,$所以$BP=BQ=\sqrt {1000^{2}-600^{2}}=800(m)$。所以$PQ=1600m$。所以村庄能听到宣讲的时间为$1600÷200=8(min)$。所以村庄总共能听到8min的宣传。
7. 在一次“综合与实践”课中,张老师设计了如下数表:
| $n$ | $2$ | $3$ | $4$ | $5$ | …$$ |
| $a$ | $2^{2}-1$ | $3^{2}-1$ | $4^{2}-1$ | $5^{2}-1$ | …$$ |
| $b$ | $4$ | $6$ | $8$ | $10$ | …$$ |
| $c$ | $2^{2}+1$ | $3^{2}+1$ | $4^{2}+1$ | $5^{2}+1$ | …$$ |
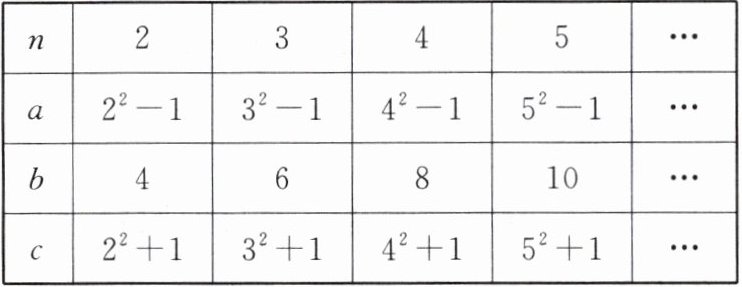
(1)请你分别观察$a,b,c与n$之间的关系,并用含自然数$n(n > 1)$的代数式表示:$a= $______,$b= $______,$c= $______。
(2)猜想:以$a,b,c$为边的三角形是否为直角三角形?并证明你的猜想。
| $n$ | $2$ | $3$ | $4$ | $5$ | …$$ |
| $a$ | $2^{2}-1$ | $3^{2}-1$ | $4^{2}-1$ | $5^{2}-1$ | …$$ |
| $b$ | $4$ | $6$ | $8$ | $10$ | …$$ |
| $c$ | $2^{2}+1$ | $3^{2}+1$ | $4^{2}+1$ | $5^{2}+1$ | …$$ |

(1)请你分别观察$a,b,c与n$之间的关系,并用含自然数$n(n > 1)$的代数式表示:$a= $______,$b= $______,$c= $______。
(2)猜想:以$a,b,c$为边的三角形是否为直角三角形?并证明你的猜想。
答案:
(1)$n^{2}-1$ 2n $n^{2}+1$
(2)解:是直角三角形。证明:因为$a^{2}+b^{2}=(n^{2}-1)^{2}+4n^{2}=n^{4}+2n^{2}+1=(n^{2}+1)^{2}=c^{2},$所以$a^{2}+b^{2}=c^{2}$。所以以a,b,c为边的三角形是直角三角形。
(1)$n^{2}-1$ 2n $n^{2}+1$
(2)解:是直角三角形。证明:因为$a^{2}+b^{2}=(n^{2}-1)^{2}+4n^{2}=n^{4}+2n^{2}+1=(n^{2}+1)^{2}=c^{2},$所以$a^{2}+b^{2}=c^{2}$。所以以a,b,c为边的三角形是直角三角形。
查看更多完整答案,请扫码查看


