《2025年同步练习册泰山出版社八年级数学上册青岛版》

5. 互为相反数的两个数的平方相等的逆命题是：______。

答案： 如果两个数的平方相等,那么这两个数互为相反数

6. 如图,小明利用两块相同的三角板,分别在三角板的边缘画直线$AB和CD$,并由此判定$AB // CD$,这是根据______,两直线平行。

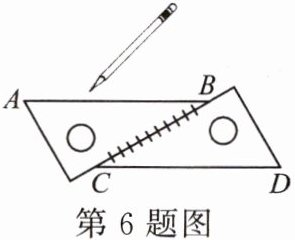
答案： 内错角相等

7. 下列命题中：①有公共顶点和一条公共边的两个角一定是邻补角；②垂直于同一条直线的两条直线互相垂直；③相等的角是对顶角；④过直线外一点有且只有一条直线与这条直线平行。其中是真命题的有______(填序号)。
三、解答题

答案： ④

8. 已知：如图,$AE平分\angle BAC$,$CE平分\angle ACD$,且$\angle \alpha + \angle \beta = 90^{\circ}$。
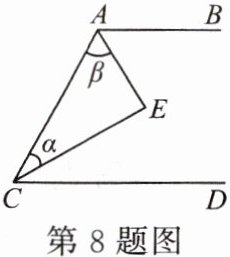
求证：$AB // CD$。

答案： 证明:因为CE平分∠ACD,所以∠ACD=2∠α。因为AE平分∠BAC,所以∠BAC=2∠β。所以∠ACD+∠BAC=2∠α+2∠β。即∠ACD+∠BAC=2(∠α+∠β)。因为∠α+∠β=90°,所以∠ACD+∠BAC=180°。所以AB//CD。

9. 如图,在$\triangle ABC$中,$\angle A : \angle ABC : \angle ACB = 3 : 4 : 5$,$BE平分\angle ABC$,$CF \perp AB于点F$,$BE和CF相交于点O$,求$\angle BOC$的度数。

答案： 解:因为∠A+∠ABC+∠ACB=180°,∠A:∠ABC:∠ACB=3:4:5,所以∠A=45°,∠ABC=60°,∠ACB=75°。因为BE平分∠ABC,所以∠OBC=$\frac{1}{2}$∠ABC=30°。因为CF⊥AB,所以∠BFC=90°。所以∠ABC+∠BCF=90°。所以∠BCF=90°-60°=30°。因为∠BOC+∠OBC+∠BCF=180°,所以∠BOC=180°-∠OBC-∠BCF=180°-30°-30°=120°。

10. 著名数学教育家G. 波利亚,有句名言：“发现问题比解决问题更重要。”这句话启发我们：要想学会数学,就需要观察、发现问题,探索问题的规律性东西,要有一双敏锐的眼睛。请先观察下列等式找出规律,并解答问题。
①$1^{3} = 1^{2}$；
②$1^{3} + 2^{3} = 3^{2}$；
③$1^{3} + 2^{3} + 3^{3} = 6^{2}$；
④$1^{3} + 2^{3} + 3^{3} + 4^{3} = 10^{2}$；
⑤$1^{3} + 2^{3} + 3^{3} + 4^{3} + 5^{3} = 15^{2}$；
......
(1)等式⑥是______；
(2)$1^{3} + 2^{3} + 3^{3} + … + n^{3} = $______($n$为正整数)；
(3)求$11^{3} + 12^{3} + 13^{3} + 14^{3} + 15^{3}$的值。

答案：
(1)1³+2³+3³+4³+5³+6³=21²
(2)(1+2+3+4+…+n)²
(3)1³+2³+3³+…+15³-(1³+2³+3³+…+10³)=(1+2+3+…+15)²-(1+2+3+4+…+10)²=120²-55²=14400-3025=11375