《2025年同步练习册泰山出版社八年级数学上册青岛版》

2. 如图,小明不小心将墨滴在作业本的数轴上,被墨迹覆盖的数可能是( )。

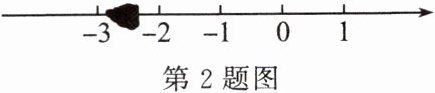
A.$\sqrt{3}$
B.$\sqrt{5}$
C.$-\sqrt{5}$
D.$-\sqrt{3}$

答案： C

3. 如图,每个小正方形的边长为1,在$\triangle ABC的三边a$,$b$,$c$中,无理数是( )。

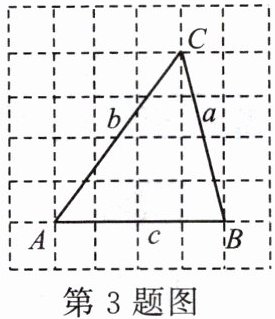
A.$a$
B.$b$,$c$
C.$c$
D.$a$,$b$,$c$

答案： A

4. 如图,$OA = OB$,点$A$表示的数是( )。

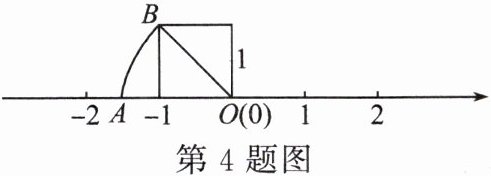
A.$\sqrt{2}$
B.$-\sqrt{2}$
C.1.5
D.$-1.5$

答案： B

5. 在数轴上到原点的距离为$\sqrt{6}$的点表示的数是______。

答案： $\pm \sqrt{6}$

6. 等腰直角三角形的腰长为3,斜边长为$a$,下列关于$a$的四种说法：①$a$是无理数；②$a$可以用数轴上的一个点表示；③$3 ＜ a ＜ 4$；④$a$是18的算术平方根。其中所有正确说法的序号为______。

答案： ①②④

7. 如图,在$4×4$的正方形网格中,每个小正方形的边长都为1。请在给定网格中分别画出长度为$\sqrt{17}$,$\sqrt{13}$,$\sqrt{20}$的线段。

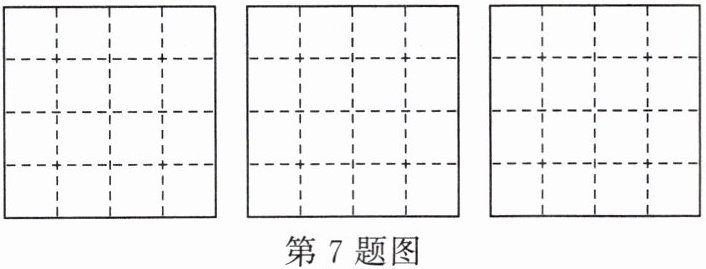
答案：
如图,图①中线段长度为$\sqrt{17}$,图②中线段长度为$\sqrt{13}$,图③中线段长度为$\sqrt{20}$。

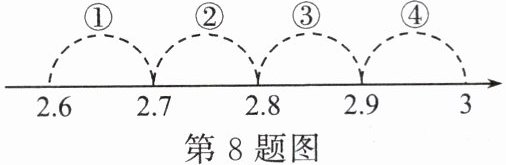
8. 如图,在数轴上标注了四段范围,表示$\sqrt{8}$的点落在( )。

A.范围①
B.范围②
C.范围③
D.范围④

答案： C 解析:因为$2.6^{2}=6.76$,$2.7^{2}=7.29$,$2.8^{2}=7.84$,$2.9^{2}=8.41$,$3^{2}=9$,且$7.84＜8＜8.41$,所以$2.8＜\sqrt{8}＜2.9$。所以表示$\sqrt{8}$的点落在范围③。

9. 【探究过程】人们在长期的数学实践中总结了许多解决数学问题的方法,形成了许多光辉的数学思想,其中转化思想是中学教学中最活跃、最实用,也是最重要的数学思想,例如将不规则图形转化为规则图形就是研究图形问题比较常用的一种方法。
问题提出：求边长分别为$\sqrt{5}$,$\sqrt{10}$,$\sqrt{13}$的三角形面积。
问题解决：
在解答这个问题时,先建立一个正方形网格(每个小正方形的边长均为1),再在网格中画出边长分别为$\sqrt{5}$,$\sqrt{10}$,$\sqrt{13}的格点三角形\triangle ABC$(如图①),$AB = \sqrt{5}$是直角边分别为1和2的直角三角形的斜边,$BC = \sqrt{10}$是直角边分别为1和3的直角三角形的斜边,$AC = \sqrt{13}$是直角边分别为2和3的直角三角形的斜边,用一个大长方形的面积减去三个直角三角形的面积,这样不需要求$\triangle ABC$的高,而借用网格就能计算它的面积。
(1)请直接写出图①中$\triangle ABC$的面积为______；
(2)类比迁移：求边长分别为$\sqrt{5}$,$\sqrt{8}$,$\sqrt{17}$的三角形面积(请利用图②的正方形网格画出相应的$\triangle ABC$,并求出它的面积)。

答案：

(1)$\frac{7}{2}$；
(2)如图,$\triangle ABC$即为所求,$S_{\triangle ABC}=4× 2-\frac{1}{2}× 4× 1-\frac{1}{2}× 2× 1-\frac{1}{2}× 2× 2=3$。