《2025年同步练习册泰山出版社八年级数学上册青岛版》

本题考查了全等三角形的判定与性质,全等三角形的判定结合全等三角形的性质是证明线段相等和角相等的重要工具。在判定三角形全等时,关键是选择恰当的判定方法,本题不要忽略公共边这个隐含条件。

答案： 假设题目为：如图，点A、B、C、D在同一直线上，$AB = DC$，$AE// BF$，且$AE = BF$，求证：$EC = FD$（需结合题意假设相应图形存在）。
答题：
证明：
因为$AE// BF$，
所以$\angle A=\angle FBD$（两直线平行，同位角相等）。
因为$AB = DC$，$AB+BC=DC+BC$，
所以$AC = BD$。
在$\triangle AEC$和$\triangle BFD$中，
$\begin{cases}AE = BF\\\angle A=\angle FBD\\AC = BD\end{cases}$
根据$SAS$（边角边）判定定理，$\triangle AEC\cong\triangle BFD$。
所以$EC = FD$（全等三角形的对应边相等）。

2. 如图,点$B$,$F$,$C$,$E$在同一条直线上,$FB = CE$,$AB// ED$,$AC// FD$,$AD交BE于点O$。求证：$AD与BE$互相平分。

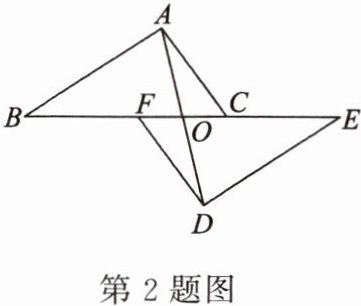
答案： 证明:因为FB=CE,
所以BC=EF。
又因为AB//ED,AC//FD,
所以∠ABC=∠DEF,∠ACB=∠DFE。
在△ABC和△DEF中,∠ABC=∠DEF,
BC=EF,
∠ACB=∠DFE,
所以△ABC≌△DEF(ASA)。
所以AC=DF。
在△AOC和△DOF中,∠AOC=∠DOF,
∠ACO=∠DFO,
AC=DF,
所以△AOC≌△DOF(AAS)。
所以AO=DO,CO=FO。
因为BF=CE,
所以BO=EO。
所以AD与BE互相平分。

例 3
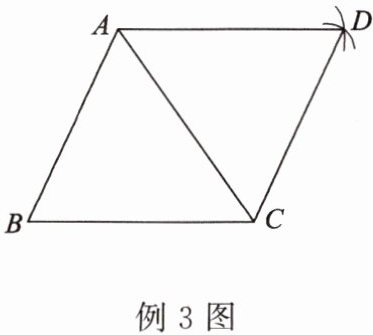
如图,以$\triangle ABC的顶点A$为圆心,以$BC$为半径作弧,再以顶点$C$为圆心,以$AB$的长为半径作弧,两弧交于点$D$,连接$AD$,$CD$。若$\angle B = 65^{\circ}$,求$\angle ADC$的度数。

答案： 解:因为以点A为圆心,以BC长为半径作弧;以顶点C为圆心,以AB长为半径作弧,两弧交于点D。
所以AB=CD,BC=AD。
在△ABC和△CDA中,
AB=CD,
BC=AD,
AC=CA,
所以△ABC≌△CDA(SSS)。
所以∠ADC=∠B=65°。

由作法可得$AB = CD$,$BC = AD$,然后证明$\triangle ABC和\triangle CDA$全等,再根据全等三角形的对应角相等解答。

答案： 在$\triangle ABC$和$\triangle CDA$中，
$AB = CD$（已知），
$BC = AD$（已知），
$AC = CA$（公共边），
根据$SSS$（三边相等）全等条件，$\triangle ABC \cong \triangle CDA$，
根据全等三角形的对应角相等，得$\angle B = \angle D$。

本题通过尺规作图考查对于全等三角形的判定与性质的掌握,解题的关键是根据作法得到全等三角形中具有相等关系的边。

答案： 假设题目为：用尺规作图作一个角等于已知角（如已知∠AOB），并通过全等三角形的判定与性质证明两角相等。以下是作答：
作法：
①以O为圆心，任意长为半径画弧，交OA于C，交OB于D；
②作射线$O^{\prime}A^{\prime}$，以$O^{\prime}$为圆心，OC长为半径画弧，交$O^{\prime}A^{\prime}$于$C^{\prime}$；
③以$C^{\prime}$为圆心，CD长为半径画弧，交前弧于$D^{\prime}$；
④过点$D^{\prime}$作射线$O^{\prime}B^{\prime}$，则$\angle A^{\prime}O^{\prime}B^{\prime}=\angle AOB$。
证明：
由作法知，在$\triangle OCD$和$\triangle O^{\prime}C^{\prime}D^{\prime}$中，
$OC = O^{\prime}C^{\prime}$，
$OD = O^{\prime}D^{\prime}$（半径相等），
$CD = C^{\prime}D^{\prime}$（半径相等），
根据“SSS”可得$\triangle OCD\cong\triangle O^{\prime}C^{\prime}D^{\prime}$，
所以$\angle AOB = \angle A^{\prime}O^{\prime}B^{\prime}$。

3. 如图,$AD// BC$,$\angle BAD = 90^{\circ}$,以点$B$为圆心,$BC$长为半径画弧,与射线$AD相交于点E$,连接$BE$,过点$C作CF\perp BE$,垂足为$F$。
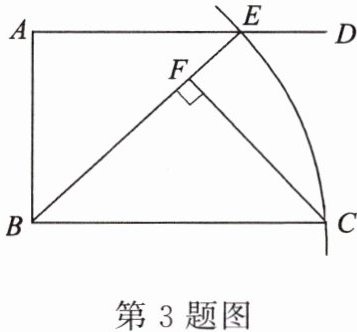
1. 线段$BF$与图中现有的哪一条线段相等？你得出的结论是：$BF = $______；
2. 证明你的结论。

答案： 1.AE
2.证明:因为CF⊥BE,
所以∠A=∠BFC=90°。
因为AD//BC,
所以∠AEB=∠FBC。
由题意得BE=BC。
在△AEB和△FBC中,∠BAD=∠BFC,
∠AEB=∠FBC,
BE=BC,
所以△AEB≌△FBC(AAS)。
所以BF=AE。

1. 如图,从下列四个条件：①$BC = B'C$；②$AC = A'C$；③$\angle A'CA = \angle B'CB$；④$AB = A'B'$中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数为( )。


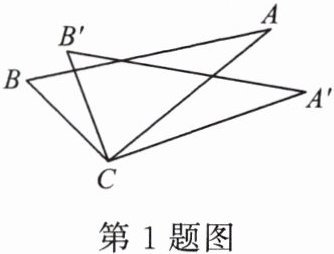
A.$1$个
B.$2$个
C.$3$个
D.$4$个

答案： B