《2025年同步练习册泰山出版社八年级数学上册青岛版》

定义：用来说明一个概念______的语句叫作这个概念的定义。

答案： 含义

定义：对某件事情______的语句叫作命题。它通常由______和______两部分组成。它常写成“______”的形式。

答案： 作出判断 条件 结论 如果……,那么……

(1)按结论成立与否可分为真命题和______。反例具备命题的______,而不符合命题的结论。

答案： 假命题 条件

(2)按命题条件和结论的关系可分为______和______,二者______关系。

答案： 原命题 逆命题 互逆

(3)按命题的获取方式可分为基本事实和______(需要证明或推导)。

答案： 定理(推论)

什么是证明：除基本事实外,其他命题的正确性都需要由基本事实、定义、已有结论及已知条件出发,通过逻辑推理的方法加以证实。推理的过程叫______。

答案： 证明

为什么证明：由观察、实验、______和______得到的命题都是一种猜想,不能保证其正确性,故需要经过严密的逻辑推理加以证实。

答案： 类比 归纳

怎样证明：证明三步骤：①根据题意,画出图形；②______；③找出由已知推出求证的途径,______。

答案： 结合图形,根据条件和结论,写出已知、求证 写出证明

(1)平行线的性质定理和______。

答案： 判定定理

(2)三角形的内角和定理：______及其推论。

答案： 三角形的内角和等于180°

(3)直角三角形的性质定理和判定定理。
(4)反证法。

答案：
(3)性质定理：①直角三角形的两个锐角互余；②直角三角形斜边上的中线等于斜边的一半。判定定理：①有一个角是直角的三角形是直角三角形；②有两个角互余的三角形是直角三角形；③一边上的中线等于这边一半的三角形是直角三角形。
(4)反证法：先假设命题结论不成立，从假设出发推理得出矛盾，判定假设错误，从而肯定原命题结论正确的证明方法。

例1 找规律是解决数学问题的一种重要的手段,而规律的找寻既需要敏锐的观察力,又需要严密的逻辑推理能力。观察如图所示的点阵图和相应的等式,探究其中的规律：
(1)在④后面的横线上写出相应的等式：

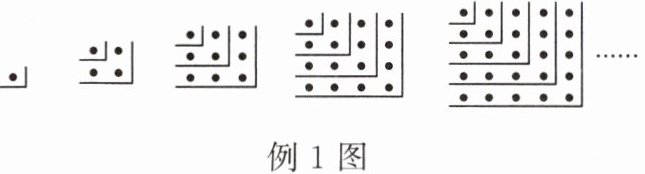
①$1 = 1^{2}$；
②$1 + 3 = 2^{2}$；
③$1 + 3 + 5 = 3^{2}$；
④______；
⑤$1 + 3 + 5 + 7 + 9 = 5^{2}$；
...
(2)请写出第$n$个等式；
(3)利用(2)中的等式,计算$11 + 13 + 15 + … + 47 + 49$。

答案：
(1)1+3+5+7=4²
(2)1+3+5+…+(2n-1)=n²
(3)(1+3+5+…+47+49)-(1+3+5+7+9)=(1+3+5+7+…+25×2-1)-(1+3+5+7+5×2-1)=25²-5²=625-25=600