《2025年同步练习册泰山出版社八年级数学上册青岛版》

1. 下列各数：$0.163,5\pi,\dfrac{19}{6},\sqrt{0.4},\dfrac{\sqrt{13}}{2},-0.10505$,其中无理数的个数是( )。

A.1
B.2
C.3
D.4

答案： C

例2 (1)$\sqrt{81}$的平方根是______；
(2)$\sqrt[3]{64}$的算术平方根是( )。
A. 8
B. $\pm8$
C. 2
D. $\pm2$

答案：
(1)$\pm3$；
(2)C

(1)$\sqrt{81}$表示什么意义？一个正数有几个平方根？
(2)$\sqrt[3]{64}$表示什么意义？如何求一个实数的立方根？

答案：
(1)
$\sqrt{81}$表示求81的算术平方根，即求一个非负数，使其平方等于81，因为$9^2 = 81$，所以$\sqrt{81}=9$。
一个正数有2个平方根，它们互为相反数。
(2)
$\sqrt[3]{64}$表示求64的立方根，即求一个数，使其立方等于64，因为$4^3 = 64$，所以$\sqrt[3]{64}=4$。
求一个实数$a$的立方根，可利用立方与开立方的互逆关系，若$x^3=a$，则$x$叫做$a$的立方根，记作$x = \sqrt[3]{a}$，也可通过查立方根表或使用计算器来求实数的立方根。

求算术平方根、平方根和立方根,有时需要对给出的数据进行化简,然后利用算术平方根、平方根和立方根的定义进行求解。

答案： 答题卡：
1. 求算术平方根：
若求$m$的算术平方根，记为$\sqrt{m}$（$m\geq0$），例如，若$m = 9$，则$\sqrt{m}=\sqrt{9}=3$。
2. 求平方根：
若求$n$的平方根，记为$\pm\sqrt{n}$（$n\geq0$），例如，若$n = 16$，则$\pm\sqrt{n}=\pm\sqrt{16}=\pm4$。
3. 求立方根：
若求$p$的立方根，记为$\sqrt[3]{p}$，例如，若$p = -8$，则$\sqrt[3]{p}=\sqrt[3]{-8}=-2$。

2. (1)$\sqrt{16}$的算术平方根是______；
(2)$\sqrt[3]{-512}$的立方根是______。

答案：
(1)2；
(2)-2

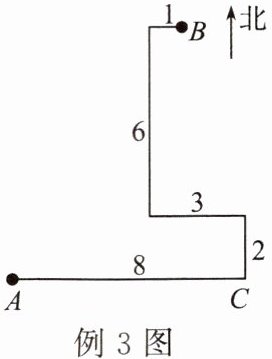
例3 小明与小亮到小岛去玩寻宝游戏。如图,他们登陆后,先向正东走了8 km,再向正北走,走了2 km,遇上礁石,只好改道向正西走,走了3 km后,再向正北走6 km,再向正东走1 km,找到了藏宝的地点。求藏宝的地点离登陆点的距离。

答案： 解:如图,过点B作BD⊥AC于点D,连接AB。在Rt△ABD中,AD=8 - 3 + 1 = 6,BD=2 + 6 = 8,由勾股定理,得AB=$\sqrt{AD^{2}+BD^{2}}$=$\sqrt{6^{2}+8^{2}}$=10(km),所以藏宝的地点离登陆点的距离是10 km。

实际问题→构造直角三角形→应用勾股定理→解决实际问题。

答案： 答题卡：
解：假设实际问题为：在一个长方体的屋顶上，从地面到屋顶的两个相对的角点之间引钢丝绳，已知长方体的高为$3$米，底面长为$4$米，宽为$3$米，求钢丝绳的长度。
构造直角三角形：
将长方体想象为由三个矩形组成，从地面到屋顶的两个相对的角点引出的钢丝绳可以看作是一个直角三角形的斜边，这个直角三角形的两个直角边分别由长方体的高和底面对角线构成。
应用勾股定理：
底面对角线长度可以通过底面的长和宽计算得出，即：
$\sqrt{4^2 + 3^2} = \sqrt{16 + 9} = \sqrt{25} = 5 (米)$
然后，利用勾股定理计算钢丝绳的长度，即直角三角形的斜边长度：
$\sqrt{3^2 + 5^2} = \sqrt{9 + 25} = \sqrt{34} \approx 5.83 (米)$
解决实际问题：
所以，钢丝绳的长度约为$5.83$米。

实际问题的解决体现了数学建模思想,即把实际问题转化为数学问题。正东方向与正北方向的夹角是直角,正西方向与正北方向的夹角也是直角,于是可以构造直角三角形,利用勾股定理来解这类题目。

答案： 点$A$到点$C$的直线距离为$5$千米。

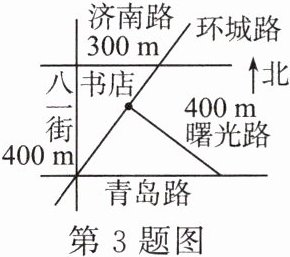
3. 如图,青岛路与济南路平行,并且与八一街垂直,曙光路与环城路垂直。如果小明站在济南路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程约为______。

答案： 500 m

例4 计算：$\left(-\dfrac{1}{2}\right)^{-2}+\sqrt[3]{8}-|1-\sqrt{9}|$。

答案： 解:原式$=(-2)^{2}+2-|1 - 3|=4 + 2 - 2 = 4$。

分别计算算式中的负指数幂、立方根、平方根以及化去绝对值符号。

答案： 答案略