《2025年同步练习册泰山出版社八年级数学上册青岛版》

实数的运算是初中阶段的基本运算,主要涉及开方(开平方、开立方)、负指数幂、零指数幂、绝对值等,涉及的知识较多,具有一定的灵活性。

答案： 答题卡：
解：
例如，计算$\sqrt{4} + 2^{-2} - (3 - \pi)^0 + |\frac{1}{2} - \sqrt{2}|$（仅作为示例题目）
$=\sqrt{4} + \frac{1}{4} - 1 + |\frac{1}{2} - \sqrt{2}|$
$= 2 + \frac{1}{4} - 1 + (\sqrt{2} - \frac{1}{2})$
$= 2 + 0.25 - 1 + \sqrt{2} - 0.5$
$= 0.75 + \sqrt{2}$
答案不唯一，如计算$4$的算术平方根为$2$；$2$的负二次幂为$\frac{1}{4}$；$3-\pi$的零次幂为$1$；$\frac{1}{2}-\sqrt{2}$绝对值为$\sqrt{2}-\frac{1}{2}$，最终结果为$0.75 + \sqrt{2}$。

4. 计算：$(-2)^2+|\sqrt{2}-1|-\sqrt[3]{27}-(\pi-3)^0$。

答案： 原式=4+($\sqrt{2}$-1)-3-1=$\sqrt{2}$-1。

1. 下列各数中,无理数是( )。

A.0
B.$\sqrt{3}$
C.$\dfrac{14}{7}$
D.$-3.14$

答案： B

2. 下列运算正确的是( )。

A.$\sqrt{36}= \pm6$
B.$\sqrt{(-4)^2}= -4$
C.$\sqrt[3]{9}= 3$
D.$\sqrt[3]{-5}= -\sqrt[3]{5}$

答案： D

3. 如图,直线$l上有三个正方形a,b,c$,若$a,c$的面积分别为5和11,则$b$的面积为( )。

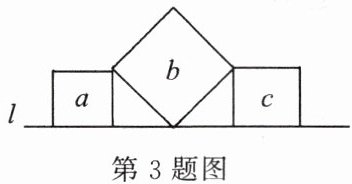
A.4
B.16
C.24
D.55

答案： B

4. 实数$a,b$在数轴上对应点的位置如图所示,则下列结论正确的是( )。


A.$|a|＜|b|$
B.$a＞b$
C.$a＜-b$
D.$|a|＞|b|$

答案： A

5. 如图,在数轴上,点$A,B$对应的实数分别为1,3,$BC\perp AB$,$BC = 1$,以$A$为圆心,$AC$为半径作弧,交数轴正半轴于点$P$,则点$P$对应的实数为( )。

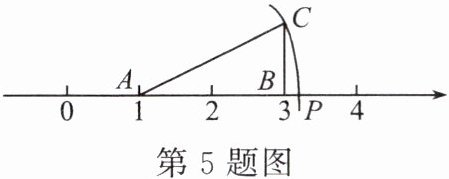
A.$\sqrt{5}+1$
B.$\sqrt{5}$
C.$\sqrt{5}+3$
D.$4-\sqrt{5}$

答案： A

6. 一个正数的平方根分别是$2a + 1和7 - a$,那么$a$的立方根是______。

答案： -2

7. 已知$\sqrt[3]{1 - 2x}与\sqrt[3]{3x - 7}$互为相反数,则$x = $______。

答案： 6

8. 计算：$|\sqrt{9} - 2|^0+(-2)^{-1}= $______。

答案： $\frac{1}{2}$

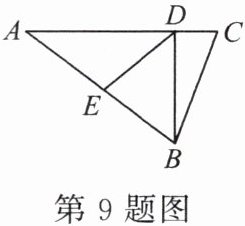
9. 如图,在$\triangle ABC$中,$AC = 21$,$BC = 13$,$D是AC$边上一点,$BD = 12$,$AD = 16$。
(1)求证：$BD\perp AC$。
(2)若$E是边AB$上的动点,求线段$DE$的最小值。

答案：
(1)证明:因为AC=21,AD=16,所以CD=AC - AD=5。在△BCD中,BD²+CD²=12²+5²=169=BC²,所以∠BDC=90°,所以BD⊥AC。
(2)解:当DE⊥AB时,DE最短,在Rt△ABD中,AB=$\sqrt{AD^{2}+BD^{2}}$=$\sqrt{16^{2}+12^{2}}$=20。因为$\frac{1}{2}$AD×DB=$\frac{1}{2}$AB×DE,所以DE=$\frac{16×12}{20}$=9.6,所以线段DE的最小值为9.6。