2025年全优方案夯实与提高七年级数学上册华师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年全优方案夯实与提高七年级数学上册华师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第20页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
9. 已知有理数$a大于有理数b$,则(
A.$a的绝对值大于b$的绝对值
B.$a的绝对值小于b$的绝对值
C.$a的相反数大于b$的相反数
D.$a的相反数小于b$的相反数
D
)。A.$a的绝对值大于b$的绝对值
B.$a的绝对值小于b$的绝对值
C.$a的相反数大于b$的相反数
D.$a的相反数小于b$的相反数
答案:
D
10. 把$-\frac{2024}{2025}$,$-\frac{2023}{2024}$,$-\frac{98}{99}$,$-\frac{97}{98}$这四个数按从小到大的顺序排列为
-$\frac{2024}{2025}$<-$\frac{2023}{2024}$<-$\frac{98}{99}$<-$\frac{97}{98}$
。
答案:
- $\frac{2024}{2025}$ < - $\frac{2023}{2024}$ < - $\frac{98}{99}$ < - $\frac{97}{98}$
11. 对于任意有理数$x$,可用$[x]表示不超过x$的最大整数,如$[2.9] = 2$。给出如下结论:
①$[-3] = -3$;②$[-2.9] = -2$;③$[0.9] = 0$;④$[x] + [-x] = 0$。其中正确的是
①$[-3] = -3$;②$[-2.9] = -2$;③$[0.9] = 0$;④$[x] + [-x] = 0$。其中正确的是
①③
(填序号)。
答案:
①③
12. 已知有理数$a$,$b$在数轴上的位置如图。
(1) 在数轴上标出$-a$,$-b$。
(2) 把$a$,$b$,$0$,$-a$,$-b$这五个数按从小到大的顺序用“$<$”连接。
(3) 用“$>$”“$<$”或“$=$”填空:$|a|$
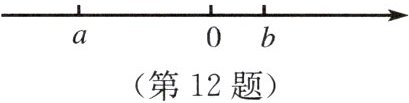
(1) 在数轴上标出$-a$,$-b$。
(2) 把$a$,$b$,$0$,$-a$,$-b$这五个数按从小到大的顺序用“$<$”连接。
(3) 用“$>$”“$<$”或“$=$”填空:$|a|$
>
$a$,$|b|$=
$b$。
(1)略.
(2)a < - b < 0 < b < - a.
(2)a < - b < 0 < b < - a.
答案:
(1)略.
(2)a < - b < 0 < b < - a.
(3) > =
(1)略.
(2)a < - b < 0 < b < - a.
(3) > =
13. 【盘锦】在有理数$1$,$\frac{1}{2}$,$-1$,$0$中,最小的数是(
A.$1$
B.$\frac{1}{2}$
C.$-1$
D.$0$
C
)。A.$1$
B.$\frac{1}{2}$
C.$-1$
D.$0$
答案:
C
14. 写出一个比$-\frac{1}{4}小且比-\frac{1}{3}$大的分数:
-$\frac{3}{10}$(答案不唯一)
。
答案:
- $\frac{3}{10}$(答案不唯一)
15. 设$x$是有理数,我们规定:$x^{+} = \begin{cases}x(x \geq 0), \\ 0(x < 0), \end{cases} $ $x^{-} = \begin{cases}0(x > 0), \\ x(x \leq 0)。 \end{cases} $例如:$3^{+} = 3$,$(-2)^{+} = 0$;$3^{-} = 0$,$(-2)^{-} = -2$。解决下列问题:
(1) $(\frac{1}{2})^{+} = $
(2) 分别用一个含$|x|$,$x的式子表示x^{+}$,$x^{-}$。
(1) $(\frac{1}{2})^{+} = $
$\frac{1}{2}$
,$(-1)^{-} = $$-1$
,$x^{+} + x^{-} = $$x$
。(2) 分别用一个含$|x|$,$x的式子表示x^{+}$,$x^{-}$。
当x≥0时,x⁺ = x,|x| = x,所以x⁺ = $\frac{x + |x|}{2}$. 当x < 0时,x⁺ = 0,|x| = - x,所以x⁺ = $\frac{x + |x|}{2}$. 综上所述,当x为有理数时,x⁺ = $\frac{x + |x|}{2}$. 当x≥0时,x⁻ = 0,|x| = x,所以x⁻ = $\frac{x - |x|}{2}$. 当x < 0时,x⁻ = x,|x| = - x,所以x⁻ = $\frac{x - |x|}{2}$. 综上所述,当x为有理数时,x⁻ = $\frac{x - |x|}{2}$.
答案:
(1)$\frac{1}{2}$ - 1 x
(2)当x≥0时,x⁺ = x,|x| = x,所以x⁺ = $\frac{x + |x|}{2}$. 当x < 0时,x⁺ = 0,|x| = - x,所以x⁺ = $\frac{x + |x|}{2}$. 综上所述,当x为有理数时,x⁺ = $\frac{x + |x|}{2}$. 当x≥0时,x⁻ = 0,|x| = x,所以x⁻ = $\frac{x - |x|}{2}$. 当x < 0时,x⁻ = x,|x| = - x,所以x⁻ = $\frac{x - |x|}{2}$. 综上所述,当x为有理数时,x⁻ = $\frac{x - |x|}{2}$.
(1)$\frac{1}{2}$ - 1 x
(2)当x≥0时,x⁺ = x,|x| = x,所以x⁺ = $\frac{x + |x|}{2}$. 当x < 0时,x⁺ = 0,|x| = - x,所以x⁺ = $\frac{x + |x|}{2}$. 综上所述,当x为有理数时,x⁺ = $\frac{x + |x|}{2}$. 当x≥0时,x⁻ = 0,|x| = x,所以x⁻ = $\frac{x - |x|}{2}$. 当x < 0时,x⁻ = x,|x| = - x,所以x⁻ = $\frac{x - |x|}{2}$. 综上所述,当x为有理数时,x⁻ = $\frac{x - |x|}{2}$.
查看更多完整答案,请扫码查看


