《2025年长江全能学案同步练习册七年级数学上册人教版》

12. 观察下列等式：
第 $ 1 $ 个等式：$ a_1 = \frac{1}{1×3} = \frac{1}{2}×(1 - \frac{1}{3}) $；
第 $ 2 $ 个等式：$ a_2 = \frac{1}{3×5} = \frac{1}{2}×(\frac{1}{3} - \frac{1}{5}) $；
第 $ 3 $ 个等式：$ a_3 = \frac{1}{5×7} = \frac{1}{2}×(\frac{1}{5} - \frac{1}{7}) $；
第 $ 4 $ 个等式：$ a_4 = \frac{1}{7×9} = \frac{1}{2}×(\frac{1}{7} - \frac{1}{9}) $；
……
请解答下列问题：
(1)按以上规律列出第 $ 5 $ 个等式：
$ a_5 = $ ；
(2)用含 $ n $ 的式子表示第 $ n $ 个等式：
$ a_n = $ （$ n $ 为正整数）；
(3)求 $ a_1 + a_2 + a_3 + a_4 + \cdots + a_{100} $ 的值。

答案：
(1)
$a_5=\frac{1}{9×11}=\frac{1}{2}×(\frac{1}{9}-\frac{1}{11})$
(2)
$a_n=\frac{1}{(2n - 1)(2n + 1)}=\frac{1}{2}×(\frac{1}{2n - 1}-\frac{1}{2n + 1})$
(3)
$\begin{align}a_1 + a_2 + a_3 + a_4 + \cdots + a_{100}&=\frac{1}{2}×(1 - \frac{1}{3})+\frac{1}{2}×(\frac{1}{3}-\frac{1}{5})+\frac{1}{2}×(\frac{1}{5}-\frac{1}{7})+\cdots+\frac{1}{2}×(\frac{1}{199}-\frac{1}{201})\\&=\frac{1}{2}×[(1 - \frac{1}{3})+(\frac{1}{3}-\frac{1}{5})+(\frac{1}{5}-\frac{1}{7})+\cdots+(\frac{1}{199}-\frac{1}{201})]\\&=\frac{1}{2}×(1 - \frac{1}{201})\\&=\frac{1}{2}×\frac{200}{201}\\&=\frac{100}{201}\end{align}$

13. (1)当 $ a = \frac{1}{2} $，$ b = \frac{1}{3} $ 时，分别求式子 $ a^2 - 2ab + b^2 $ 与 $ (a - b)^2 $ 的值；
(2)当 $ a = 5 $，$ b = 3 $ 时，分别求式子 $ a^2 - 2ab + b^2 $ 与 $ (a - b)^2 $ 的值；
(3)观察(1)(2)中式子 $ a^2 - 2ab + b^2 $ 与 $ (a - b)^2 $ 的值，猜想 $ a^2 - 2ab + b^2 $ 与 $ (a - b)^2 $ 有何关系；
(4)利用你的猜想，尝试求 $ 2024^2 - 2×2024×2025 + 2025^2 $ 的值。

答案：
(1)
当$a = \frac{1}{2}$，$b = \frac{1}{3}$时：
$a^{2}-2ab + b^{2}=(\frac{1}{2})^{2}-2×\frac{1}{2}×\frac{1}{3}+(\frac{1}{3})^{2}=\frac{1}{4}-\frac{1}{3}+\frac{1}{9}=\frac{9 - 12+4}{36}=\frac{1}{36}$；
$(a - b)^{2}=(\frac{1}{2}-\frac{1}{3})^{2}=(\frac{1}{6})^{2}=\frac{1}{36}$。
(2)
当$a = 5$，$b = 3$时：
$a^{2}-2ab + b^{2}=5^{2}-2×5×3 + 3^{2}=25-30 + 9=4$；
$(a - b)^{2}=(5 - 3)^{2}=2^{2}=4$。
(3)
通过
(1)
(2)中计算结果可知$a^{2}-2ab + b^{2}=(a - b)^{2}$。
(4)
由$a^{2}-2ab + b^{2}=(a - b)^{2}$，令$a = 2024$，$b = 2025$，则：
$2024^{2}-2×2024×2025+2025^{2}=(2024 - 2025)^{2}=(-1)^{2}=1$。

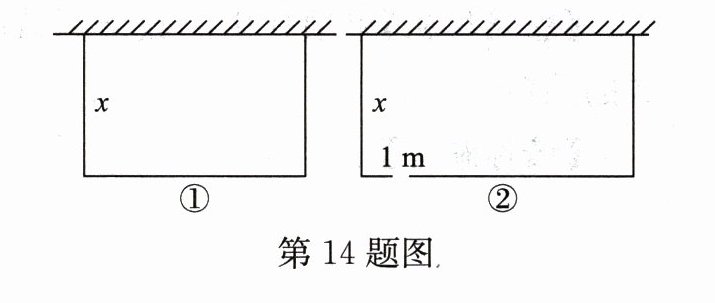
14. 修建一个长方形的花园，花园一边靠墙(墙足够长)，另外三边用 $ a $ m 长的建筑材料围成，其中与墙垂直的一边长为 $ x $。
(1)如图①，用代数式表示：
①与墙相对的一边长为 $ m $；
②花园的面积为 $ m^2 $；
(2)如图②，与墙相对的一边开有 $ 1m $ 宽的门(不用建筑材料)。
①用代数式表示长方形花园的面积 $ S $；
②当 $ a = 30 $，$ x = 5 $ 时，求 $ S $ 的值。

答案：
(1)① $a - 2x$
② $x(a - 2x)$
(2)① $S = x(a - 2x + 1)$
② 当 $a = 30$，$x = 5$ 时，$S = 5×(30 - 2×5 + 1) = 5×21 = 105$