第114页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
6. 有两种消费券:A券,满60元减20元;B券,满90元减30元,即一次购物大于或等于60元,付款时减20元;一次购物大于或等于90元,付款时减30元.小敏有一张A券,小聪有一张B券,他们都购买了一件标价相同的商品,各自付款.若能用券时用券,这样两人共付款150元,则所购买商品的标价是
85或100
元.
答案:
85或100
7. 某家电商场销售A,B两种品牌的冰箱,5月份A品牌冰箱的销售量为80台,B品牌的销售量为120台,6月份A品牌冰箱的销售量减少了5%,但总销售量增长了16%.问:B品牌冰箱6月份的销售量比5月份增长了百分之几?
答案:
设B品牌冰箱6月份的销售量比5月份增长的百分数为$x$。
5月份A,B两种品牌冰箱的总销售量为$80 + 120 = 200(台)$。
6月份A品牌冰箱的销售量为$80 × (1 - 5\%) = 76(台)$。
6月份B品牌冰箱的销售量为$120 × (1 + x)(台)$。
6月份A,B两种品牌冰箱的总销售量为$200 × (1 + 16\%) = 232(台)$。
根据6月份A,B两种品牌冰箱的总销售量,可以列出方程:
$76 + 120 × (1 + x) = 232$,
$120x=232-76-120$,
$120x = 36$,
$x = 0.3$。
将$0.3$转换为百分比形式,即 $30\%$。
答:B品牌冰箱6月份的销售量比5月份增长了$30\%$。
5月份A,B两种品牌冰箱的总销售量为$80 + 120 = 200(台)$。
6月份A品牌冰箱的销售量为$80 × (1 - 5\%) = 76(台)$。
6月份B品牌冰箱的销售量为$120 × (1 + x)(台)$。
6月份A,B两种品牌冰箱的总销售量为$200 × (1 + 16\%) = 232(台)$。
根据6月份A,B两种品牌冰箱的总销售量,可以列出方程:
$76 + 120 × (1 + x) = 232$,
$120x=232-76-120$,
$120x = 36$,
$x = 0.3$。
将$0.3$转换为百分比形式,即 $30\%$。
答:B品牌冰箱6月份的销售量比5月份增长了$30\%$。
8. 为了准备小颖六年后上大学的学费15000元,她的父母现在就参加了教育储蓄,下面有两种储蓄方式:

方式一:先存三年期的,三年后将本息和自动转存三年期;
方式二:直接存六年期的.
你认为哪种储蓄方式开始存入的本金比较少?

方式一:先存三年期的,三年后将本息和自动转存三年期;
方式二:直接存六年期的.
你认为哪种储蓄方式开始存入的本金比较少?
答案:
设方式一开始存入本金$x$元,方式二开始存入本金$y$元。
方式一:
根据利息公式:$本息和 = 本金+本金×年利率×时间$,先存三年,本息和为$x + x× 3.24\%× 3=x(1 + 3.24\%× 3)$,再转存三年,则有:
$x(1 + 3.24\%× 3)(1 + 3.24\%× 3)=15000$
$x×(1 + 0.0972)^{2}=15000$
$x×1.0972^{2}=15000$
$x=\frac{15000}{1.0972^{2}}\approx12460.47$(元)
方式二:
根据公式$本息和 = 本金+本金×年利率×时间$,可得$y(1 + 3.60\%× 6)=15000$
$y×(1+0.216)=15000$
$y×1.216 = 15000$
$y=\frac{15000}{1.216}\approx12335.53$(元)
因为$12335.53\lt12460.47$,所以方式二开始存入的本金比较少。
答:方式二开始存入的本金比较少。
方式一:
根据利息公式:$本息和 = 本金+本金×年利率×时间$,先存三年,本息和为$x + x× 3.24\%× 3=x(1 + 3.24\%× 3)$,再转存三年,则有:
$x(1 + 3.24\%× 3)(1 + 3.24\%× 3)=15000$
$x×(1 + 0.0972)^{2}=15000$
$x×1.0972^{2}=15000$
$x=\frac{15000}{1.0972^{2}}\approx12460.47$(元)
方式二:
根据公式$本息和 = 本金+本金×年利率×时间$,可得$y(1 + 3.60\%× 6)=15000$
$y×(1+0.216)=15000$
$y×1.216 = 15000$
$y=\frac{15000}{1.216}\approx12335.53$(元)
因为$12335.53\lt12460.47$,所以方式二开始存入的本金比较少。
答:方式二开始存入的本金比较少。
9. 某电视台组织知识竞赛,共设20道选择题,各题分值相同、每题必答,下表记录了五位参赛者的得分情况.
|参赛者|A|B|C|D|E|
|答对题数|20|19|18|14|m|
|得分|100|94|88|n|40|
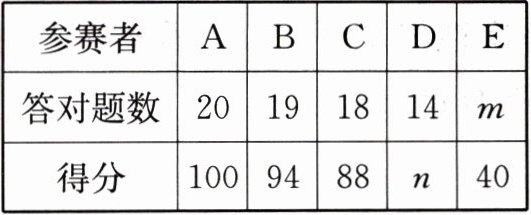$
根据表格提供的信息解答下列问题:
(1)每做对一题得______分,每做错一题得______分;
(2)直接写出m= ______,n= ______;
(3)参赛者G说他得了80分,你认为可能吗?为什么?
(1)每做对一题得
(2)直接写出m=
(3)参赛者G说他得了80分,你认为可能吗?为什么?
|参赛者|A|B|C|D|E|
|答对题数|20|19|18|14|m|
|得分|100|94|88|n|40|
$
根据表格提供的信息解答下列问题:
(1)每做对一题得______分,每做错一题得______分;
(2)直接写出m= ______,n= ______;
(3)参赛者G说他得了80分,你认为可能吗?为什么?
(1)每做对一题得
5
分,每做错一题得-1
分;(2)直接写出m=
10
,n=64
;(3)参赛者G说他得了80分,你认为可能吗?为什么?
不可能,理由如下:假设G得80分可能,设G答对k题,则5k-(20 - k)=80,5k - 20 + k = 80,6k = 100,k=50/3,不是整数,所以不可能。
答案:
(1)设做对一题得$x$分,做错一题得$y$分。
由$A$答对$20$题得$100$分,可得$20x = 100$,解得$x = 5$。
$B$答对$19$题,做错$1$题,得$94$分,则$19x + y = 94$,把$x = 5$代入,$19×5 + y = 94$,解得$y = - 1$。
所以每做对一题得$5$分,每做错一题得$-1$分。
(2)
$D$答对$14$题,做错$20 - 14 = 6$题,$n = 14×5 - 6×1 = 64$。
$E$得$40$分,设$E$答对$m$题,则$5m-(20 - m)=40$,
$5m - 20 + m = 40$,
$6m = 60$,
$m = 10$。
所以$m = 10$,$n = 64$。
(3)假设$G$得$80$分可能,设$G$答对$k$题,则$5k-(20 - k)=80$,
$5k - 20 + k = 80$,
$6k = 100$,
$k=\frac{50}{3}$,不是整数,所以不可能。
综上,答案依次为:
(1)$5$,$-1$;
(2)$10$,$64$;
(3)不可能,理由如上述计算$k$不为整数。
(1)设做对一题得$x$分,做错一题得$y$分。
由$A$答对$20$题得$100$分,可得$20x = 100$,解得$x = 5$。
$B$答对$19$题,做错$1$题,得$94$分,则$19x + y = 94$,把$x = 5$代入,$19×5 + y = 94$,解得$y = - 1$。
所以每做对一题得$5$分,每做错一题得$-1$分。
(2)
$D$答对$14$题,做错$20 - 14 = 6$题,$n = 14×5 - 6×1 = 64$。
$E$得$40$分,设$E$答对$m$题,则$5m-(20 - m)=40$,
$5m - 20 + m = 40$,
$6m = 60$,
$m = 10$。
所以$m = 10$,$n = 64$。
(3)假设$G$得$80$分可能,设$G$答对$k$题,则$5k-(20 - k)=80$,
$5k - 20 + k = 80$,
$6k = 100$,
$k=\frac{50}{3}$,不是整数,所以不可能。
综上,答案依次为:
(1)$5$,$-1$;
(2)$10$,$64$;
(3)不可能,理由如上述计算$k$不为整数。
10. 某市已经全面实行了居民新型合作医疗保险制度,享受医保的居民可在规定的医院就医,并按规定标准报销部分医疗费用,下表是医疗费用报销的标准:

若家住幸福社区的王爷爷在一次住院中个人自付了住院医疗费5000元(自付医疗费= 实际医疗费-按标准报销的金额),则他在这一次住院中的实际医疗费用为多少元?

若家住幸福社区的王爷爷在一次住院中个人自付了住院医疗费5000元(自付医疗费= 实际医疗费-按标准报销的金额),则他在这一次住院中的实际医疗费用为多少元?
答案:
设王爷爷的实际医疗费用为$x$元。
情况1:$x \leq 5000$
报销比例70%,自付费用为$x - 70\%x = 30\%x$。
最大自付费用:$5000 × 30\% = 1500$元。
$1500 < 5000$,不符合题意,排除。
情况2:$5000 < x \leq 10000$
分段自付:5000元部分自付$5000 × (1 - 70\%) = 1500$元;
超过5000元部分$(x - 5000)$自付$20\%$,自付费用为$1500 + 20\%(x - 5000)$。
最大自付费用($x=10000$时):$1500 + 20\%×5000 = 2500$元。
$2500 < 5000$,不符合题意,排除。
情况3:$x > 10000$
分段自付:
5000元部分:$5000 × (1 - 70\%) = 1500$元;
5000~10000元部分:$5000 × (1 - 80\%) = 1000$元;
超过10000元部分$(x - 10000)$:$10\%(x - 10000)$。
总自付费用:$1500 + 1000 + 10\%(x - 10000) = 5000$。
解方程:
$2500 + 0.1(x - 10000) = 5000$
$0.1(x - 10000) = 2500$
$x - 10000 = 25000$
$x = 35000$。
结论:实际医疗费用为$35000$元。
$\boxed{35000}$
情况1:$x \leq 5000$
报销比例70%,自付费用为$x - 70\%x = 30\%x$。
最大自付费用:$5000 × 30\% = 1500$元。
$1500 < 5000$,不符合题意,排除。
情况2:$5000 < x \leq 10000$
分段自付:5000元部分自付$5000 × (1 - 70\%) = 1500$元;
超过5000元部分$(x - 5000)$自付$20\%$,自付费用为$1500 + 20\%(x - 5000)$。
最大自付费用($x=10000$时):$1500 + 20\%×5000 = 2500$元。
$2500 < 5000$,不符合题意,排除。
情况3:$x > 10000$
分段自付:
5000元部分:$5000 × (1 - 70\%) = 1500$元;
5000~10000元部分:$5000 × (1 - 80\%) = 1000$元;
超过10000元部分$(x - 10000)$:$10\%(x - 10000)$。
总自付费用:$1500 + 1000 + 10\%(x - 10000) = 5000$。
解方程:
$2500 + 0.1(x - 10000) = 5000$
$0.1(x - 10000) = 2500$
$x - 10000 = 25000$
$x = 35000$。
结论:实际医疗费用为$35000$元。
$\boxed{35000}$
查看更多完整答案,请扫码查看


