第73页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
5. 如图 1,$ A $,$ B $ 两村之间有一条两岸互相平行的河,河宽为 $ a $. 现要在河上造一座桥(桥必须与河岸垂直),使 $ A $,$ B $ 之间的路程最短,试画出造桥位置. 对于此题,我们可以这样解决:
如图 2,把点 $ A $ 向下平移河宽 $ a $ 到点 $ A' $,连接 $ A'B $ 交 $ l_2 $ 于点 $ C $;过点 $ C $ 作 $ CD \perp l_1 $ 于点 $ D $,则 $ CD $ 就是造桥位置.
请仿照以上材料,解决如下问题:
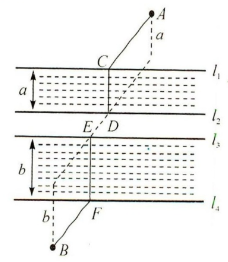
如图 3,$ A $,$ B $ 两村之间有两条互相平行的河. 一条河宽 $ a $,另一条河宽 $ b $,现欲在两条河上各造一座桥(桥必须与河岸垂直),使 $ A $,$ B $ 之间的路程最短,试画出造桥位置.

如图 2,把点 $ A $ 向下平移河宽 $ a $ 到点 $ A' $,连接 $ A'B $ 交 $ l_2 $ 于点 $ C $;过点 $ C $ 作 $ CD \perp l_1 $ 于点 $ D $,则 $ CD $ 就是造桥位置.
请仿照以上材料,解决如下问题:
如图 3,$ A $,$ B $ 两村之间有两条互相平行的河. 一条河宽 $ a $,另一条河宽 $ b $,现欲在两条河上各造一座桥(桥必须与河岸垂直),使 $ A $,$ B $ 之间的路程最短,试画出造桥位置.

答案:

6. 【问题情景】如图 1,在平面直角坐标系中,$ A(3,0) $,$ B(1,3) $,在 $ y $ 轴上找一点 $ C $,使得 $ AC + BC $ 的值最小,请探究点 $ C $ 的坐标.
【方法分析】小刚的做法是先画出点 $ A $ 关于 $ y $ 轴的对称点 $ A' $,连接 $ A'B $ 交 $ y $ 轴于点 $ C $,则此时 $ AC + BC $ 的值最小. 请在图 1 中按照小刚的方法完成作图. 小刚进一步发现:连接 $ OB $,利用 $ S_{\triangle A'OB} = S_{\triangle A'OC} + S_{\triangle BOC} $ 列方程,可求出点 $ C $ 的坐标. 请按照小刚的思路求出点 $ C $ 的坐标.
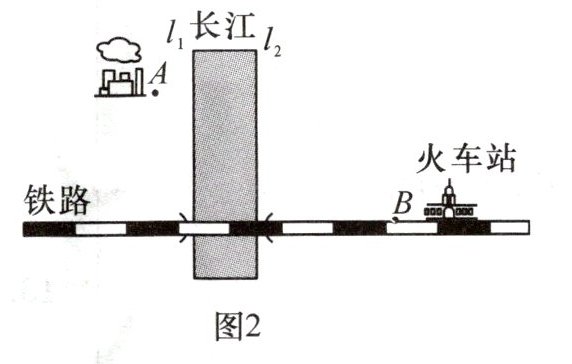
【问题解决】为响应“秉承节能减排理念,共筑生态环保家园”的号召,现考虑为某化工厂设计一个工业运输用桥方案(平面示意图如图 2). 假定长江两岸为互相平行的直线 $ l_1 $,$ l_2 $,且 $ l_1 $ 与 $ l_2 $ 相距 $ 1200\ m $,铁路所在直线垂直于 $ l_1 $. 位于点 $ A $ 处的化工厂与 $ l_1 $ 相距 $ 600\ m $,与铁路相距 $ 2400\ m $,位于点 $ B $ 处的火车站与 $ l_2 $ 相距 $ 2400\ m $. 若桥与长江两岸垂直,则在何处修建运输桥可以使 $ A $,$ B $ 两点之间的路径最短?请你完成作图,并通过计算求出桥与铁路的距离.

【方法分析】小刚的做法是先画出点 $ A $ 关于 $ y $ 轴的对称点 $ A' $,连接 $ A'B $ 交 $ y $ 轴于点 $ C $,则此时 $ AC + BC $ 的值最小. 请在图 1 中按照小刚的方法完成作图. 小刚进一步发现:连接 $ OB $,利用 $ S_{\triangle A'OB} = S_{\triangle A'OC} + S_{\triangle BOC} $ 列方程,可求出点 $ C $ 的坐标. 请按照小刚的思路求出点 $ C $ 的坐标.
【问题解决】为响应“秉承节能减排理念,共筑生态环保家园”的号召,现考虑为某化工厂设计一个工业运输用桥方案(平面示意图如图 2). 假定长江两岸为互相平行的直线 $ l_1 $,$ l_2 $,且 $ l_1 $ 与 $ l_2 $ 相距 $ 1200\ m $,铁路所在直线垂直于 $ l_1 $. 位于点 $ A $ 处的化工厂与 $ l_1 $ 相距 $ 600\ m $,与铁路相距 $ 2400\ m $,位于点 $ B $ 处的火车站与 $ l_2 $ 相距 $ 2400\ m $. 若桥与长江两岸垂直,则在何处修建运输桥可以使 $ A $,$ B $ 两点之间的路径最短?请你完成作图,并通过计算求出桥与铁路的距离.


答案:
∴OA'=3.
∵S△A'OB=S△A'OC+S△BOC,
∴$\frac{1}{2}× 3× 3=\frac{1}{2}× 3× OC+\frac{1}{2}× OC× 1$.
∴OC=$\frac{9}{4}$.
∴C(0,$\frac{9}{4}$).【问题解决】图略,将点A向右平移1200 m至点A',连接A'B交l₂于点N,作MN⊥l₂交l₁于点M,则桥修在MN处.作A'E⊥MN,交MN于点D,交铁路所在的直线于点E,设l₂与铁路交于点F.设DE=NF=x m.
∵S△A'BE=S△NBF+S梯形AFEN,
∴$\frac{1}{2}× 2400× 3000=\frac{1}{2}× 2400\cdot x+\frac{1}{2}× 600(x+2400)$,解得x=1920.
∴桥与铁路的距离为1920 m.
6. 【方法分析】图略.由题意,得A'O=AO,A(3,0),
∴OA'=3.
∵S△A'OB=S△A'OC+S△BOC,
∴$\frac{1}{2}× 3× 3=\frac{1}{2}× 3× OC+\frac{1}{2}× OC× 1$.
∴OC=$\frac{9}{4}$.
∴C(0,$\frac{9}{4}$).【问题解决】图略,将点A向右平移1200 m至点A',连接A'B交l₂于点N,作MN⊥l₂交l₁于点M,则桥修在MN处.作A'E⊥MN,交MN于点D,交铁路所在的直线于点E,设l₂与铁路交于点F.设DE=NF=x m.
∵S△A'BE=S△NBF+S梯形AFEN,
∴$\frac{1}{2}× 2400× 3000=\frac{1}{2}× 2400\cdot x+\frac{1}{2}× 600(x+2400)$,解得x=1920.
∴桥与铁路的距离为1920 m.
查看更多完整答案,请扫码查看


