第53页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
11. 新考向 跨学科 如图,这是蜡烛的平面镜成像原理图,以水平面为 $ x $ 轴,镜面侧面为 $ y $ 轴(镜面厚度忽略不计)建立平面直角坐标系.若某时刻火焰顶端 $ S $ 的坐标是 $ (x - 2,2) $,此时对应的虚像 $ S' $ 的坐标是 $ (3,y) $,则 $ 3x + y = $(

A.$ 1 $
B.$ 0 $
C.$ -1 $
D.$ -2 $
C
)
A.$ 1 $
B.$ 0 $
C.$ -1 $
D.$ -2 $
答案:
C
12. 已知图形 $ A $ 全部在 $ x $ 轴的上方,若将图形 $ A $ 上所有点的纵坐标都乘 $ -1 $,横坐标不变得到图形 $ B $,则(
A.两个图形关于 $ x $ 轴对称
B.两个图形关于 $ y $ 轴对称
C.两个图形重合
D.两个图形不关于任何一条直线对称
A
)A.两个图形关于 $ x $ 轴对称
B.两个图形关于 $ y $ 轴对称
C.两个图形重合
D.两个图形不关于任何一条直线对称
答案:
A
13. (2023·合肥包河区期末)如图,在 $ 3×3 $ 的正方形网格中有四个格点 $ A $, $ B $, $ C $, $ D $,以其中一个点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点可能是(
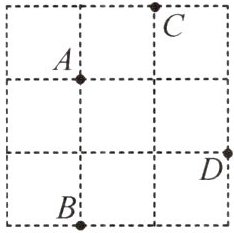
A.点 $ A $
B.点 $ B $
C.点 $ C $
D.点 $ D $
D
)
A.点 $ A $
B.点 $ B $
C.点 $ C $
D.点 $ D $
答案:
D
14. 若点 $ M(1 - 2m,m - 1) $ 关于 $ y $ 轴对称的点在第四象限,则 $ m $ 的取值范围为
0.5<m<1
.
答案:
0.5<m<1
15. 已知点 $ A(a,b) $ 和点 $ B(c,d)(c \neq 0,d \neq 0) $ 关于 $ x $ 轴对称,则 $ 3b + 3d + \frac{2a}{c} = $
2
.
答案:
2
16. 清华附中校本经典题 在如图所示的正方形网格中建立平面直角坐标系, $ \triangle ABC $ 的顶点坐标分别为 $ A(-5,2) $, $ B(-3,1) $, $ C(-1,5) $,请按要求解答下列问题:
(1) 画出 $ \triangle ABC $ 关于 $ x $ 轴对称的 $ \triangle A_1B_1C_1 $,并写出点 $ A $ 的对应点 $ A_1 $ 的坐标为(
(2) 直线 $ l $ 上各点的横坐标都是 $ 1 $,作出 $ \triangle ABC $ 关于直线 $ l $ 对称的 $ \triangle A_2B_2C_2 $,并直接写出点 $ A_2 $, $ B_2 $, $ C_2 $ 的坐标: $ A_2 $(
(3) 若 $ Q(a,b) $ 是 $ \triangle ABC $ 内任意一点,则它关于直线 $ l $ 对称的点 $ Q_1 $ 的坐标为

(1) 画出 $ \triangle ABC $ 关于 $ x $ 轴对称的 $ \triangle A_1B_1C_1 $,并写出点 $ A $ 的对应点 $ A_1 $ 的坐标为(
-5
,-2
).(2) 直线 $ l $ 上各点的横坐标都是 $ 1 $,作出 $ \triangle ABC $ 关于直线 $ l $ 对称的 $ \triangle A_2B_2C_2 $,并直接写出点 $ A_2 $, $ B_2 $, $ C_2 $ 的坐标: $ A_2 $(
7
,2
), $ B_2 $(5
,1
), $ C_2 $(3
,5
).(3) 若 $ Q(a,b) $ 是 $ \triangle ABC $ 内任意一点,则它关于直线 $ l $ 对称的点 $ Q_1 $ 的坐标为
(2-a,b)
(用含 $ a $, $ b $ 的代数式表示).
答案:
解: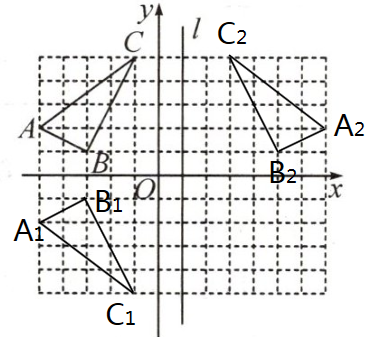
(1)-5 -2
(2)7 2 5 1 3 5
(3)(2-a,b)
解:

(1)-5 -2
(2)7 2 5 1 3 5
(3)(2-a,b)
17. 新考向 推理能力 如图,在平面直角坐标系中,对 $ \triangle ABC $ 进行循环往复的轴对称变换.若原来点 $ A $ 的坐标为 $ (1,2) $,则经过第 $ 2025 $ 次变换后点 $ A $ 的对应点的坐标为(

A.$ (1,-2) $
B.$ (-1,-2) $
C.$ (-1,2) $
D.$ (1,2) $
C
)
A.$ (1,-2) $
B.$ (-1,-2) $
C.$ (-1,2) $
D.$ (1,2) $
答案:
C
查看更多完整答案,请扫码查看


