第18页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. 如图,在$\triangle ABC$中,$AB = BC = AC$,$BD\perp AC$,垂足为$D$,点$E$在边$BC$的延长线上,且有$CE = CD$,$DB = DE$。
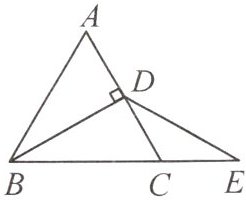
(1) 以点$C$为顶点的三角形有
(2)图中的等腰三角形有
(3) 图中的直角三角形有

(1) 以点$C$为顶点的三角形有
△ABC,△CBD,△CDE
;以$CD$为边的三角形有△CBD,△CDE
。(2)图中的等腰三角形有
△ABC,△CDE,△BDE
;等边三角形有△ABC
。(3) 图中的直角三角形有
△ABD,△CBD
;钝角三角形有△CDE,△BDE
。
答案:
1.
(1)△ABC,△CBD,△CDE △CBD,△CDE
(2)△ABC,△CDE,△BDE △ABC
(3)△ABD,△CBD △CDE,△BDE
(1)△ABC,△CBD,△CDE △CBD,△CDE
(2)△ABC,△CDE,△BDE △ABC
(3)△ABD,△CBD △CDE,△BDE
2. (2024·淮南五校联考期中) 港珠澳大桥全长约 55 公里,集桥、岛、隧于一体,是连接香港、珠海和澳门的超大型跨海通道,是迄今世界最长的跨海大桥。如图所示的是港珠澳大桥中的斜拉索桥,索塔、斜拉索、桥面构成了三角形,这样使其更稳定,其中运用的数学原理是

三角形具有稳定性
。
答案:
2.三角形具有稳定性
3. (2023·淮南期中) 若一个三角形的两边长分别为 2 cm,7 cm,则它的第三边的长可能是(
A.2 cm
B.3 cm
C.6 cm
D.9 cm
C
)A.2 cm
B.3 cm
C.6 cm
D.9 cm
答案:
3.C
4. 小明想做一个三角形的框架,他有两根长度分别为 4 cm 和 6 cm 的细木条,需要将其中一根木条分为两段。若不考虑损耗和接头部分,则可以分成两段的是(
A.4 cm 的木条
B.6 cm 的木条
C.两根都可以
D.两根都不行
B
)A.4 cm 的木条
B.6 cm 的木条
C.两根都可以
D.两根都不行
答案:
4.B
5. 如图,在$\triangle ABC$中,$AD$是高,$AE$是角平分线,$AF$是中线,则下列说法错误的是(
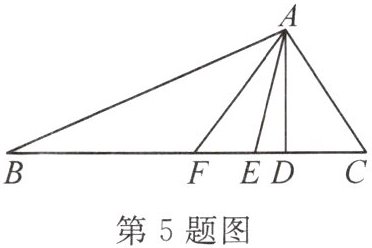
A.$BF = CF$
B.$\angle C + \angle CAD = 90°$
C.$\angle BAF = \angle CAF$
D.$S_{\triangle ABC} = 2S_{\triangle ABF}$
C
)
A.$BF = CF$
B.$\angle C + \angle CAD = 90°$
C.$\angle BAF = \angle CAF$
D.$S_{\triangle ABC} = 2S_{\triangle ABF}$
答案:
5.C
6. (2024·阜阳期末) 如图,在$\triangle ABC$中,$AD$,$AE$分别是边$BC$上的中线和高,$AE = 3 cm$,$S_{\triangle ABD} = 6 cm^2$,则$CD$的长是
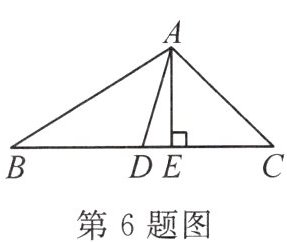
4 cm
。
答案:
6.4 cm
7. (2023·合肥包河区期末) 若三角形的三个内角度数之比为$2:3:5$,则这个三角形一定是(
A.等腰直角三角形
B.锐角三角形
C.直角三角形
D.钝角三角形
C
)A.等腰直角三角形
B.锐角三角形
C.直角三角形
D.钝角三角形
答案:
7.C
8. (2023·聊城) 如图,分别过$\triangle ABC$的顶点$A$,$B$作$AD// BE$。若$\angle CAD = 25°$,$\angle EBC = 80°$,则$\angle ACB$的度数为(
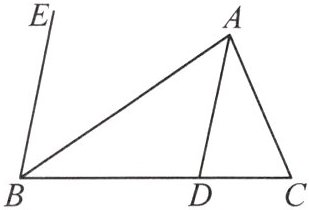
A.$65°$
B.$75°$
C.$85°$
D.$95°$
B
)
A.$65°$
B.$75°$
C.$85°$
D.$95°$
答案:
8.B
9. (2024·芜湖十校联考期中) 将一副直角三角板按如图所示的方式放置,使含$30°$角的三角板的短直角边和含$45°$角的三角板的一条直角边对齐,则$\angle 1$的度数为(
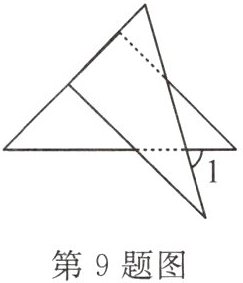
A.$30°$
B.$45°$
C.$60°$
D.$75°$
D
)
A.$30°$
B.$45°$
C.$60°$
D.$75°$
答案:
9.D
10. (2024·芜湖无为市期中) 如图,在$Rt\triangle ABC$中,$\angle C = 90°$,$AE$,$BD$是角平分线,则$\angle 1$的度数是
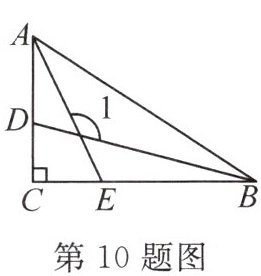
135°
。
答案:
10.135°
查看更多完整答案,请扫码查看


