第10页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
8. 华师二附中校本经典题 新考向 真实情境 如图,这是一个建筑工地的三角形支撑架ABC,它的上部∠ACB被一个长方形钢架遮挡,测量得∠A=60°,∠B=80°,则被遮挡的∠ACB的度数为(
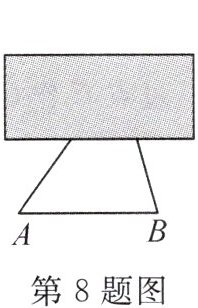
A.30°
B.40°
C.50°
D.60°
B
)
A.30°
B.40°
C.50°
D.60°
答案:
8.B
9. (教材P12例2变式)如图,B岛在A岛的南偏西55°方向,B岛在C岛的北偏西60°方向,C岛在A岛的南偏东30°方向,则从B岛看A,C两岛的视角∠ABC的度数为
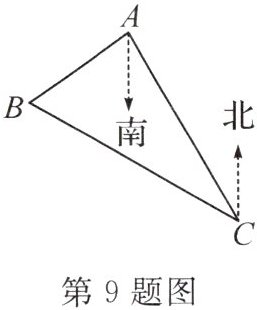
65°
.
答案:
9.65°
10. 如图,在△ABC中,P是△ABC三条角平分线的交点,则∠PBC+∠PCA+∠PAB=(
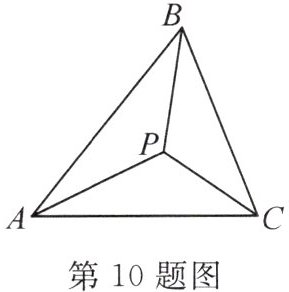
A.45°
B.120°
C.180°
D.90°
D
)
A.45°
B.120°
C.180°
D.90°
答案:
10.D
11. 北师大附属实验校本经典题 如图,在△ABC中,∠A=70°,∠C=30°,BD平分∠ABC交AC于点D,DE//AB,交BC于点E,则∠BDE的度数是(
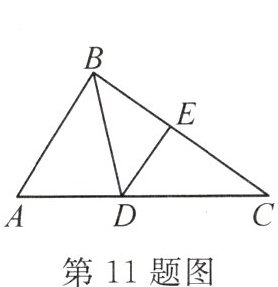
A.30°
B.40°
C.50°
D.60°
B
)
A.30°
B.40°
C.50°
D.60°
答案:
11.B
12. 新考向 真实情境 (本课时T8变式)如图,直线a,b相交所成的角跑到画板外面了,某同学发现只要量出画板的边l分别与直线a,b相交所形成的角的度数就可求得该角.已知∠1=71°,∠2=78°,则直线a,b相交所形成的锐角的度数为
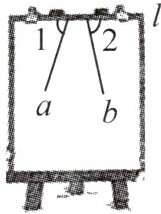
31°
.
答案:
12.31°
13. 北京五中校本经典题 如图,在△ABC中,O是△ABC角平分线的交点.已知∠ABC=60°,∠ACB=80°,求∠BOC的度数.
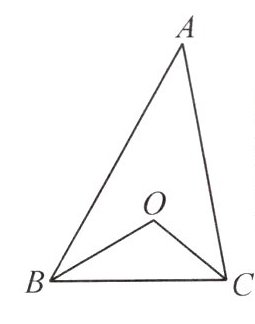

答案:
13.解:
∵O是△ABC角平分线的交点,
∴∠OBC=𝟏/𝟐∠ABC=𝟏/𝟐×60°=30°,∠OCB=𝟏/𝟐∠ACB=𝟏/𝟐×80°=40°.
∴∠BOC=180°-∠OBC-∠OCB=180°-30°-40°=110°.
∵O是△ABC角平分线的交点,
∴∠OBC=𝟏/𝟐∠ABC=𝟏/𝟐×60°=30°,∠OCB=𝟏/𝟐∠ACB=𝟏/𝟐×80°=40°.
∴∠BOC=180°-∠OBC-∠OCB=180°-30°-40°=110°.
【拓展变式1】 如图,在△ABC中,BE,CD为角平分线,且交点为O.若∠BOC=120°,则∠A的度数为
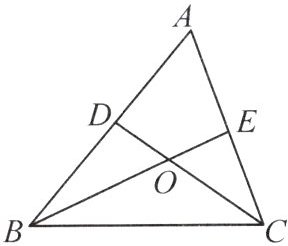
【拓展变式2】 试猜想上题中∠A与∠BOC的数量关系:若∠A=α,则∠BOC的度数为
60°
.
【拓展变式2】 试猜想上题中∠A与∠BOC的数量关系:若∠A=α,则∠BOC的度数为
90°+𝟏/𝟐α
.
答案:
【拓展变式1】 60°【拓展变式2】 90°+𝟏/𝟐α
14. 石家庄外国语校本经典题 如图,△ABC是一张纸片,把∠C沿DE折叠,使点C落在点C'的位置.
(1)当∠C=45°时,求∠1+∠2的度数.
(2)若∠C=α,请直接写出∠1+∠2的度数.(用含α的代数式表示)
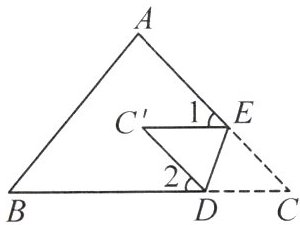
(1)当∠C=45°时,求∠1+∠2的度数.
(2)若∠C=α,请直接写出∠1+∠2的度数.(用含α的代数式表示)

答案:
14.解:
(1)
∵∠C=45°,∠CDE+∠CED+∠C=180°,
∴∠CDE+∠CED=180°-45°=135°.由折叠可知,∠CDE=∠C'DE,∠CED=∠C'ED.
∴∠C'DE+∠C'ED=∠CDE+∠CED=135°.
∴∠1+∠2=360°-(∠CDE+∠CED)-(∠C'DE+∠C'ED)=360°-135°-135°=90°.
(2)∠1+∠2=2α.
(1)
∵∠C=45°,∠CDE+∠CED+∠C=180°,
∴∠CDE+∠CED=180°-45°=135°.由折叠可知,∠CDE=∠C'DE,∠CED=∠C'ED.
∴∠C'DE+∠C'ED=∠CDE+∠CED=135°.
∴∠1+∠2=360°-(∠CDE+∠CED)-(∠C'DE+∠C'ED)=360°-135°-135°=90°.
(2)∠1+∠2=2α.
查看更多完整答案,请扫码查看


