《2025年名校课堂八年级数学上册人教版安徽专版》

9. 新考向 真实情境 图1是一乐谱架，利用立杆可进行高度调节，图2是其底座部分的平面图，其中支撑杆AB=AC，点E，F分别为AB，AC的中点，ED，FD是连接立杆和支撑杆的支架，且ED=FD. 立杆在伸缩过程中，总有△AED≌△AFD，其判定依据是(B)



A.SAS
B.SSS
C.ASA
D.AAS

答案： 9. B

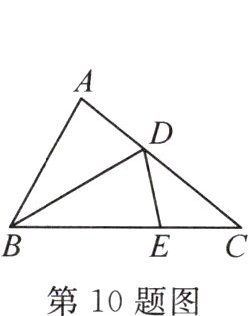
10. 如图，在△ABC中，E是边BC上一点，且AB=EB，点D在AC上，连接BD，DE. 若AD=ED，∠A=80°，∠CDE=40°，则∠C的度数为40°.

答案： 10. 40°

11. 新考向 传统文化 风筝又称“纸鸢”“风鸢”等，起源于中国东周春秋时期，距今已有2000多年的历史. 如图，这是一款风筝骨架的简化图，已知AB=AD，BC=CD，AC=90 cm，BD=60 cm，制作这个风筝需要的布料至少为2700cm².

答案： 11. 2700

12. （2024·内江）如图，点A，D，B，E在同一条直线上，AD=BE，AC=DF，BC=EF.
（1）求证：△ABC≌△DEF.

（2）若∠A=55°，∠E=45°，求∠F的度数.

答案： 12. 解：
(1)证明：
∵ AD=BE，
∴ AD+BD=BE+BD，即 AB=DE. 在△ABC 和△DEF 中，
{AB=DE,
AC=DF,
BC=EF,
∴△ABC≌△DEF(SSS).
(2)由
(1)可知，△ABC≌△DEF，
∴∠FDE=∠A=55°. 又
∵∠E=45°，
∴∠F=180°-(∠FDE+∠E)=180°-(55°+45°)=80°.

13. （2023·铜陵铜官区期末）如图，点E，F在BD上，且AB=CD，BF=DE，AE=CF. 求证：AC与BD互相平分.

答案： 13. 证明：
∵ BF=DE，
∴ BF-EF=DE-EF，即 BE=DF. 在△ABE 和△CDF 中，
{AB=CD,
BE=DF,
AE=CF,
∴△ABE≌△CDF(SSS).
∴∠B=∠D. 在△ABO 和△CDO 中，
{∠AOB=∠COD,
∠B=∠D,
AB=CD,
∴△ABO≌△CDO(AAS).
∴ AO=CO，BO=DO.
∴ AC 与 BD 互相平分.

14. 如图，AC，BD相交于点O，且AB=DC，AC=DB. 求证：OB=OC.

答案： 14. 证明：连接 BC. 在△ABC 和△DCB 中，
{AB=DC,
AC=DB,
BC=CB,
∴△ABC≌△DCB(SSS).
∴∠A=∠D. 在△AOB 和△DOC 中，
{∠AOB=∠DOC,
∠A=∠D,
AB=DC,
∴△AOB≌△DOC(AAS).
∴ OB=OC.