第44页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. (2024·淮南潘集区期末)如图,$\triangle ABC \cong \triangle ADE$,点$D$在边$BC$上,$\angle E = 35^{\circ}$,$\angle DAC = 30^{\circ}$,则$\angle BDA$的度数为
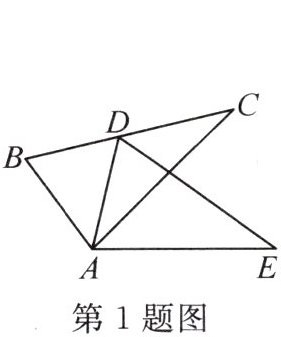
65°
。
答案:
65°
2. (2024·芜湖期中)如图,在$5 × 5$的网格中,点$M$,$N$,$A$,$B$,$C$都在格点(网格线的交点)上. 若$\triangle MNP \cong \triangle ABC$,则点$P$与点

F
重合. (填“$D$”“$E$”或“$F$”)
答案:
F
3. (2024·阜阳期中)如图,在四边形$ABCD$中,$AB = AD$,$AB \perp AD$,$AC \perp DC$,过点$B$作$BE \perp CA$,垂足为$E$。若$CD = 2$,$CE = 4$,则$BE$的长是
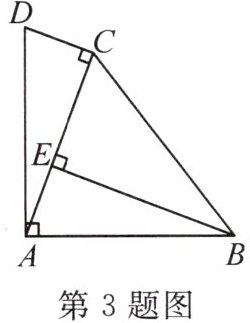
6
。
答案:
6
4. (2024·芜湖无为市期中)如图,在$Rt \triangle ABC$中,$\angle B = 90^{\circ}$,点$E$在边$AB$上,$DE = CD$,$DF \perp AC$于点$F$,$BE = CF$。若$AB = 12$,$BD = 4$,$\triangle ABC$的面积是$54$,则线段$AC$的长为(
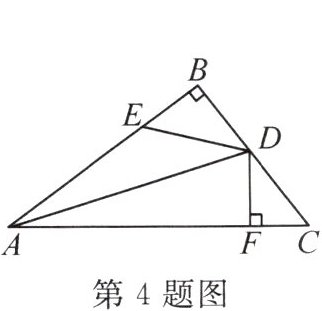
A.$13$
B.$15$
C.$16$
D.$18$
B
)
A.$13$
B.$15$
C.$16$
D.$18$
答案:
B
5. (2024·安徽)在凸五边形$ABCDE$中,$AB = AE$,$BC = DE$,$F$是$CD$的中点. 下列条件中,不能推出$AF$与$CD$一定垂直的是(
A.$\angle ABC = \angle AED$
B.$\angle BAF = \angle EAF$
C.$\angle BCF = \angle EDF$
D.$\angle ABD = \angle AEC$
D
)A.$\angle ABC = \angle AED$
B.$\angle BAF = \angle EAF$
C.$\angle BCF = \angle EDF$
D.$\angle ABD = \angle AEC$
答案:
D
6. (2024·淮南凤台县期中)如图,在$\triangle ABC$中,$AD$平分$\angle BAC$交$BC$于点$D$,$CE \perp AD$,分别交$AB$,$AD$于点$E$,$F$。
(1) 求证:$EF = CF$。
(2) 若$\angle ACB = 60^{\circ}$,$\angle BCE = 20^{\circ}$,求$\angle ABC$的度数。
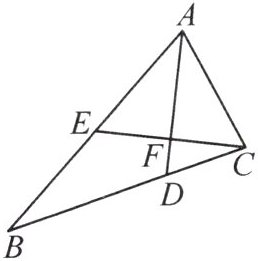
(1) 求证:$EF = CF$。
(2) 若$\angle ACB = 60^{\circ}$,$\angle BCE = 20^{\circ}$,求$\angle ABC$的度数。

答案:
解:
(1)证明:
∵AD平分∠BAC,CE⊥AD,
∴∠EAF=∠CAF,∠AFE=∠AFC=90°.在△AEF和△ACF中,{∠EAF=∠CAF,AF=AF,∠AFE=∠AFC,
∴△AEF≌△ACF(ASA).
∴EF=CF.
(2)
∵∠ACB=60°,∠BCE=20°,
∴∠ACE=∠ACB-∠BCE=40°.
∵△AEF≌△ACF,
∴∠AEC=∠ACE=40°.
∵∠AEC=∠ABC+∠BCE,
∴∠ABC=∠AEC-∠BCE=40°-20°=20°.
(1)证明:
∵AD平分∠BAC,CE⊥AD,
∴∠EAF=∠CAF,∠AFE=∠AFC=90°.在△AEF和△ACF中,{∠EAF=∠CAF,AF=AF,∠AFE=∠AFC,
∴△AEF≌△ACF(ASA).
∴EF=CF.
(2)
∵∠ACB=60°,∠BCE=20°,
∴∠ACE=∠ACB-∠BCE=40°.
∵△AEF≌△ACF,
∴∠AEC=∠ACE=40°.
∵∠AEC=∠ABC+∠BCE,
∴∠ABC=∠AEC-∠BCE=40°-20°=20°.
7. (2024·合肥瑶海区期末)如图,有两个长度相等的滑梯靠在一面竖直的墙上,其中左边滑梯的高度$AC$与右边滑梯水平方向的长度$DF$相等. 若$DF = 6\ m$,$DE = 8\ m$,$AD = 4\ m$,则$BF =$
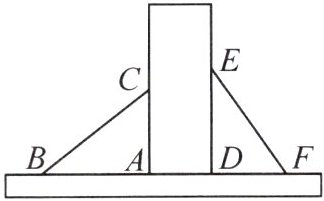
18
。
答案:
18
8. 新考向 传统文化(2024·阜阳实验中学期末)莆仙戏是我国现存最古老的地方戏曲剧种之一,被誉为“宋元南戏的活化石”,莆仙戏《踏伞行》中的“油纸伞”无疑是最重要的道具. “油纸伞”的制作工艺十分巧妙. 如图,伞圈$D$沿着伞柄滑动时,总有伞骨$BD = CD$,$AB = AC$,从而使得伞柄$AP$始终平分同一平面内两条伞骨所成的$\angle BAC$,请说明理由。
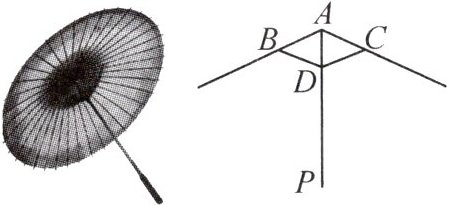

答案:
解:理由:在△ABD和△ACD中,{AB=AC,AD=AD,BD=CD,
∴△ABD≌△ACD(SSS).
∴∠BAD=∠CAD,即AP平分∠BAC.
∴△ABD≌△ACD(SSS).
∴∠BAD=∠CAD,即AP平分∠BAC.
查看更多完整答案,请扫码查看


