第55页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
12. 有一个问题:如图 1,已知 $\angle AOB$,只用无刻度的直尺和圆规判断 $\angle AOB$ 是否为直角.小意同学的方法如下:如图 2,在 $OA$,$OB$ 上分别取点 $C$,$D$,以点 $C$ 为圆心,$CD$ 的长为半径画弧,交 $OB$ 的反向延长线于点 $E$,若测量得 $OE = OD$,则 $\angle AOB = 90^{\circ}$.小意同学判断的依据是
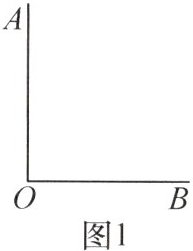
 ]
]
等腰三角形“三线合一”
.
 ]
]
答案:
等腰三角形“三线合一”
13. 新考向 真实情境 某平板电脑支架的示意图如图所示,其中 $AB = CD$,$EA = ED$,为了使用的舒适性,可调整 $\angle AEC$ 的大小.若 $\angle AEC$ 增大 $16^{\circ}$,则 $\angle BDE$ 的变化情况是(

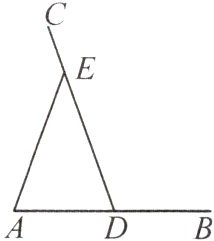
A.增大 $16^{\circ}$
B.减小 $16^{\circ}$
C.增大 $8^{\circ}$
D.减小 $8^{\circ}$
]
D
)

A.增大 $16^{\circ}$
B.减小 $16^{\circ}$
C.增大 $8^{\circ}$
D.减小 $8^{\circ}$
]
答案:
D
14. 新考向 数学文化 (2024·芜湖无为市期末)“三等分角”大约是在公元前五世纪由古希腊人提出来的.借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒 $OA$,$OB$ 组成,两根棒在点 $O$ 处相连并可绕点 $O$ 转动,点 $C$ 固定,使 $OC = CD = DE$,点 $D$,$E$ 可在槽中滑动.若 $\angle BDE = 69^{\circ}$,则 $\angle CDE$ 的度数是(
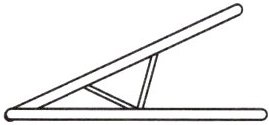
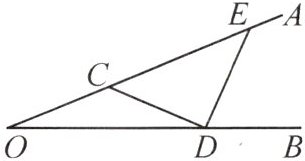
A.$60^{\circ}$
B.$69^{\circ}$
C.$76^{\circ}$
D.$88^{\circ}$
]
D
)

A.$60^{\circ}$
B.$69^{\circ}$
C.$76^{\circ}$
D.$88^{\circ}$
]
答案:
D
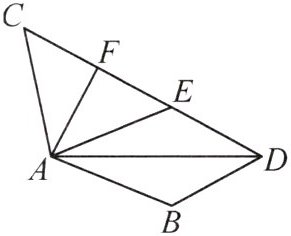
15. (2024·阜阳颍州区期末)如图,$AB = AC$,点 $B$ 关于 $AD$ 的对称点 $E$ 恰好落在 $CD$ 上,$\angle BAC = 124^{\circ}$,$AF$ 为 $\triangle ACE$ 中边 $CE$ 上的中线,则 $\angle ADB$ 的度数为(
A.$24^{\circ}$
B.$28^{\circ}$
C.$30^{\circ}$
D.$38^{\circ}$
]
B
)
A.$24^{\circ}$
B.$28^{\circ}$
C.$30^{\circ}$
D.$38^{\circ}$
]
答案:
B
16. 【方程思想】(2024·合肥期末)如图,在 $\triangle ABC$ 中,$AB = AC$,$AD = DE = EB$,$BC = BD$,求 $\angle A$ 的度数.
 ]
]
 ]
]
答案:
解:
∵DE=EB,
∴设∠BDE=∠ABD=x°.
∴∠AED=∠BDE+∠ABD=2x°.
∵AD=DE,
∴∠A=∠AED=2x°.
∴∠BDC=∠A+∠ABD=3x°.
∵BD=BC,
∴∠C=∠BDC=3x°.
∵AB=AC,
∴∠ABC=∠C=3x°.在△ABC中,∠A+∠ABC+∠C=180°,
∴3x+3x+2x=180,解得x=22.5.
∴∠A=45°.
∵DE=EB,
∴设∠BDE=∠ABD=x°.
∴∠AED=∠BDE+∠ABD=2x°.
∵AD=DE,
∴∠A=∠AED=2x°.
∴∠BDC=∠A+∠ABD=3x°.
∵BD=BC,
∴∠C=∠BDC=3x°.
∵AB=AC,
∴∠ABC=∠C=3x°.在△ABC中,∠A+∠ABC+∠C=180°,
∴3x+3x+2x=180,解得x=22.5.
∴∠A=45°.
17. 如图,在 $\triangle ABC$ 中,$AB = AC$,$AB$ 的垂直平分线交 $AB$ 于点 $N$,交 $BC$ 的延长线于点 $M$.
(1)若 $\angle A = 30^{\circ}$,求 $\angle NMB$ 的度数.
(2)如果将(1)中 $\angle A$ 的度数改为 $80^{\circ}$,其余条件不变,则 $\angle NMB$ 的度数为
(3)你发现 $\angle A$ 与 $\angle NMB$ 有什么数量关系,直接写出你的结论.
 ]
]
(1)若 $\angle A = 30^{\circ}$,求 $\angle NMB$ 的度数.
(2)如果将(1)中 $\angle A$ 的度数改为 $80^{\circ}$,其余条件不变,则 $\angle NMB$ 的度数为
40°
.(3)你发现 $\angle A$ 与 $\angle NMB$ 有什么数量关系,直接写出你的结论.
 ]
]
答案:
解:
(1)
∵AB=AC,
∴∠B=∠ACB.
∴∠B=$\frac{1}{2}$(180°-∠A)=$\frac{1}{2}$×(180°-30°)=75°.
∵MN⊥AB,
∴∠NMB=90°-∠B=90°-75°=15°.
(2)40°
(3)∠NMB=$\frac{1}{2}$∠A.理由如下:
∵AB=AC,
∴∠B=∠ACB.
∴∠B=$\frac{1}{2}$(180°-∠A)=90°-$\frac{1}{2}$∠A.
∵MN⊥AB,
∴∠NMB=90°-∠B=90°-(90°-$\frac{1}{2}$∠A)=$\frac{1}{2}$∠A.
(1)
∵AB=AC,
∴∠B=∠ACB.
∴∠B=$\frac{1}{2}$(180°-∠A)=$\frac{1}{2}$×(180°-30°)=75°.
∵MN⊥AB,
∴∠NMB=90°-∠B=90°-75°=15°.
(2)40°
(3)∠NMB=$\frac{1}{2}$∠A.理由如下:
∵AB=AC,
∴∠B=∠ACB.
∴∠B=$\frac{1}{2}$(180°-∠A)=90°-$\frac{1}{2}$∠A.
∵MN⊥AB,
∴∠NMB=90°-∠B=90°-(90°-$\frac{1}{2}$∠A)=$\frac{1}{2}$∠A.
查看更多完整答案,请扫码查看


